Vektor in der Ebene und Raum

In diesem Artikel kümmern wir uns um die Grundlagen der Vektorrechnung. Dabei zeigen wir euch zunächst, was ein ebener und was ein räumlicher Vektor ist.

Stellt euch vor, ihr steht auf einem Marktplatz und wollt in eine gewisse Richtung laufen. Und dies sollt ihr nun Mathematisch beschreiben. Eine Möglichkeit wäre: 4 Meter vorwärts laufen und 3 Meter nach rechts laufen. Genau so eine Bewegung lässt sich als Vektor darstellen. Dabei muss man sich darüber im klaren sein, ob man sich auf einer Ebene bewegt, oder ob man sich im Raum (also auch mit Höhenänderung) bewegt.

Ebener Vektor (2D)

Die folgende Grafik zeigt einen ebenen Vektor in der 2D-Ebene. Seht euch das Bild erst einmal kurz an und lest dann die Erklärungen unterhalb:

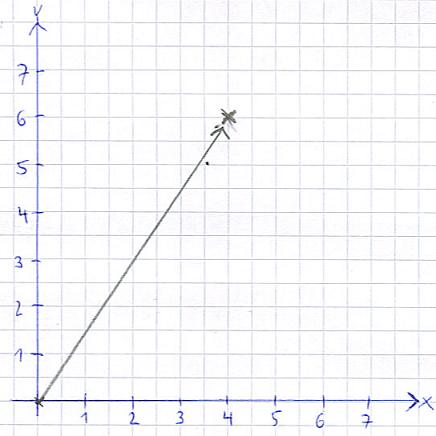
Stellt euch vor, der Punkt x = 0 und y = 0 ist der Startpunkt, an dem ihr los lauft. Geht ihr insgesamt um 4 Meter nach rechts und dabei auch um 6 Meter nach oben, erreicht Ihr den Punkt 4;6. Der Pfeil vom Ursprung auf diesen neuen Punkt wird Vektor genannt. Im nun Folgenden seht ihr die mathematische Darstellung. Dabei ist der oberste Wert der x-Wert, der untere der y-Wert:

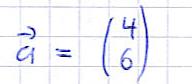
Räumlicher Vektor (3D)

Wenn wir uns nicht nur in der Länge und Breite, sondern auch in der Höhe bewegen können, brauchen wir noch eine dritte Angabe um die Richtung zu bestimmen. Diese wird dann zum Beispiel in ein x-y-z-Koordinatensystem eingetragen.

Noch ein Hinweis: Ich erhalte öfters einmal E-Mails mit verschiedenen Vorschlägen für die Achsenbeschriftungen, in denen verschiedenste x, y und z Achsen vorgeschlagen werden. In der Praxis sieht es so aus, dass man die Achsen entsprechend der Aufgabenstellung beschriftet. Außerdem gibt es rechts- und linkshändige Koordinatensysteme. Die folgende Grafik zeigt eine von vielen möglichen Achsenbeschriftungen an:

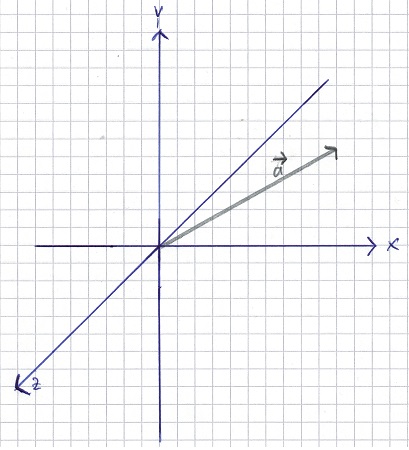
Für den Vektor langt nun keine x-y-Angabe mehr. Deshalb wird nun ein dreidimensionaler Vektor genutzt. Der oberste Wert ist hierbei der x-Wert, der mittlere der y-Wert und der unterste der z-Wert. Dies sieht dann so aus:

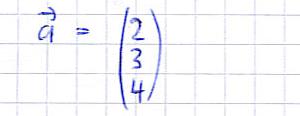
Links:

• Zur Vektorrechnung: Addition, Subtraktion, Skalarpodukt
• Zur Vektor-Übersicht
• Zur Mathematik-Übersicht