Determinante berechnen

Mit Determinanten beschäftigen wir uns in diesem Artikel der Mathematik. Dabei erklären wir zunächst, wofür man diese überhaupt braucht und gehen anschließend auf zweireihige und dreireihige Determinanten ein.

Bevor wir mit den Determinanten richtig loslegen, solltet ihr einen kurzen Check eurer Vorkenntnisse durchführen. Wenn euch die folgenden Themen noch gar nichts sagen, dann lest bitte die entsprechenden Themen erst einmal durch. Das Wissen aus diesen hilft euch sicher beim Verständnis der Determinanten.

• Lineare Gleichungssysteme
• Matrix und Matrizen Grundlagen
• Matrix: Gleichungssysteme lösen

Die Determinante: Einsatzgebiet

Bei der Lösung von naturwissenschaftlich-technischen Problemen stößt man immer wieder auf lineare Gleichungssysteme. Hat man ein solches Gleichungssystem aufgestellt, fragt man sich häufig: Ist dieses überhaupt lösbar? Bei der Beantwortung dieser Frage hilft die sogenannte Determinante weiter.

Bevor wir mit den zweireihigen Determinanten starten,  solltet ihr euch zwei Dinge merken:

• Die Elemente einer Matrix werden stets in runde Klammern geschrieben, die Elemente einer Determinante hingegen zwischen zwei senkrechte Striche.
• Eine Matrix ist ein geordnetes Zahlenschema, eine Determinante hingegen repräsentiert einen Zahlenwert.

Zweireihige Determinante

Im nun Folgenden betrachten wir eine Matrix, zu welcher wir die entsprechende Determinante berechnen möchten. Dafür gebe ich nun zunächst die allgemeine Formel an.

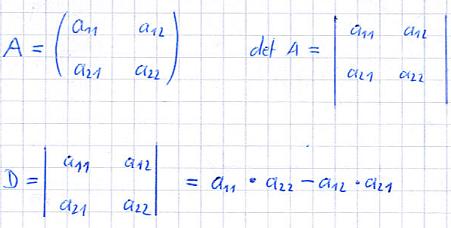
Für die Elemente a₁₁, a₁₂, a₂₁ und a₂₂ müssen nun einfach nur entsprechende Werte eingesetzt werden, mit welchen die Determinante berechnet wird. Dies gilt nur für die zweireihige Determinante!

Beispiel:

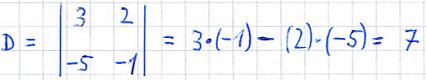
Merke: Ein lineares Gleichungssystem mit zwei Gleichungen und zwei Unbekannten besitzt genau eine Lösung, wenn die Determinante nicht verschwindet.

Dreireihige Determinante

Werfen wir nun einen Blick auf eine dreireihige Determinante. Auch hier zunächst das allgemeine Aussehen einer solchen Determinante sowie die Berechnung dieser:

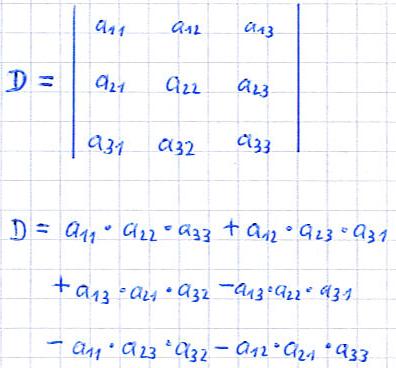
Wie auch im Fall der zweireihigen Determinante müssen hier für die einzelnen Elemente schlicht und ergreifend die Zahlen in die Berechnungsgleichung eingesetzt werden. Dies gilt nur für die dreireihige Determinante!

Links:

• Zur Mathematik Übersicht