Das Distributivgesetz wird in diesem Artikel mit Beispielen erklärt. Dabei lernst du wie man Klammern ausmultipliziert oder Klammern erzeugt. Das Distributivgesetz kommt im Zusammenhang mit Addition, Subtraktion, Multiplikation und Division vor. Die Lerninhalte liegen als Text und als Video vor.
Bevor es an die Formeln und Beispiele geht zunächst eine kurze Erklärung was man unter dem Distributivgesetz versteht.
Hinweis:
Das Distributivgesetz wird eingesetzt um Klammern ausmultiplizieren zu können oder Klammern zu erzeugen. Das Distributivgesetz - auch Verteilungsgesetz genannt - kommt im Zusammenhang mit allen Grundrechenarten vor.
Wird in der Grundschule oder spätestens in der 5. Klasse im Mathematik-Unterricht mit dem Distributivgesetz gestartet, so werden zunächst zwei Gleichungen bzw. Formeln behandelt. Beide Gleichungen dienen dazu eine Klammer aufzulösen. Als Ergebnis erhalten wir zwei Produkte (a mal b und a mal c) mit einem Pluszeichen dazwischen.
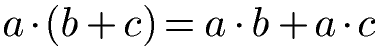
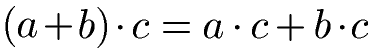
Die obere Gleichung mit der Variablen a vorne wird als linksdistributiv bezeichnet. Kommt erst eine Klammer gefolgt von einer Multiplikation mit der Variablen c so wird dies als rechtsdistributiv bezeichnet.
Distributivgesetz Addition
In diesem Abschnitt sehen wir uns typische Beispiele zum Ausmultiplizieren von Klammern mit dem Distributivgesetz an. Ziel ist es Klammern auszumultiplizieren um eine Summe zu erzeugen.
Distributivgesetz Addition Beispiel:
Nehmen wir die natürlichen Zahlen 3 und 4, welche in einer Klammer addiert werden. Davor steht eine 2 und ein Malzeichen. Um die Klammer aufzulösen, verwenden wir die Gleichung zum Distributivgesetz. Diese besagt, dass die 2 vor der Klammer sowohl mit der 3 als auch mit der 4 innerhalb der Klammer multipliziert werden muss. Im Anschluss sollte die Regel Punkt vor Strich beachtet werden. Daher zunächst 2 · 3 und 2 · 4 und erst danach 6 + 8 = 14.
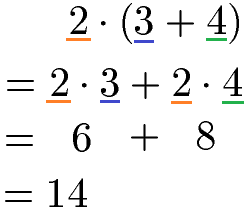
Grafische Veranschaulichung:
Das Distributivgesetz kann grafisch veranschaulicht werden. So können zwei Flächen einzeln betrachtet werden oder diese können zusammengelegt werden. Die Fläche von einem Rechteck ist Länge mal Breite. Im oberen Fall a · b für die orangene Fläche und a · c für die grüne Fläche. Diese beiden Flächen sind so groß wie die Seite a multipliziert mit (b + c) für das große Rechteck.
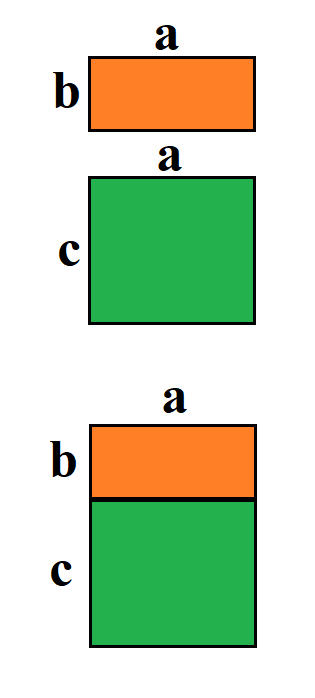
Die Flächen der Rechtecke lassen sich daher wie folgt angeben:
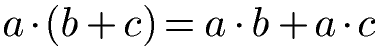
Distributivgesetz mit Brüchen:
Das Distributivgesetz lässt sich ebenfalls bei Brüchen anwenden. Der Bruch vor der Klammer wird mit jedem Summanden innerhalb der Klammer multipliziert. Nach dem Auflösen der Klammer werden die Brüche jeweils miteinander multipliziert: Zähler mal Zähler und Nenner mal Nenner. Als Ergebnis erhalten wir zwei Brüche mit gleichem Nenner bei denen einfach nur die Zähler addiert werden müssen. Als letzten Schritt wird der Bruch vollständig mit 4 gekürzt.
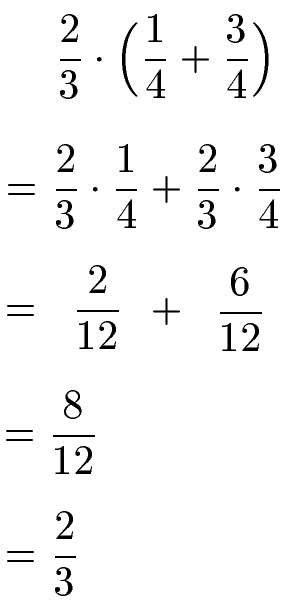
Distributivgesetz mit Variablen:
Stehen an den einzelnen Stellen nicht Zahlen sondern Variablen (Buchstaben) ändert sich am Ablauf der Berechnung dennoch nichts. Das nächste Beispiel zeigt eine Mischung aus Zahlen und Variablen. Die 3x vor der Klammer wird sowohl mit 8y als auch mit 4x multipliziert. Im Anschluss kann noch zusammengefasst werden.
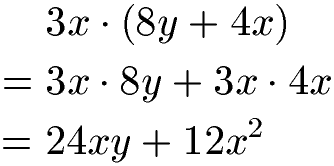
Distributivgesetz Subtraktion
In der Klammer kann anstatt eines Pluszeichens auch ein Minuszeichen vorkommen. Manche Schüler bezeichnen dies als "Distributivgesetz mit minus". Die Gleichung ändert sich dahingegen, dass eine Differenz in der Klammer vorkommt als auch eine Differenz nach dem Ausmultiplizieren. Die Formeln lauten:
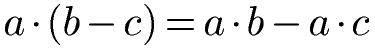
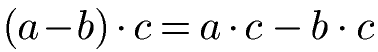
Distributivgesetz Subtraktion mit positiven Zahlen:
Kommen nur positive Zahlen vor ähnelt die Berechnung sehr stark den vorigen Beispielen. Achtet jedoch auf das Minuszeichen.
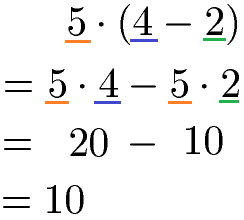
Distributivgesetz Subtraktion mit negativen Zahlen:
Werden negative Zahlen verwendet, muss man sehr aufpassen. Im nächsten Beispiel ist die -5 vor der Klammer eine negative Zahl. In der Klammer gibt es die negative Zahl -2. Dahinter folgt das Zeichen für die Subtraktion (Minuszeichen) und die Zahl 6. Beim Ausmultiplizieren der Klammer daher erst einmal -5 mal der -2 in der Klammer. Danach das Minuszeichen welches ihr von der Formel zum Distributivgesetz kennt. Gefolgt wird dies von der -5 vor der Klammer multipliziert mit der +6 in der Klammer.
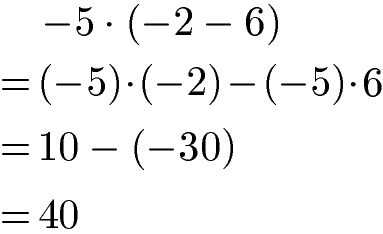
Beachte: Das Minuszeichen zwischen -2 und 6 ist das Zeichen für die Subtraktion und nicht das Vorzeichen von der 6. Im Anschluss gilt Punkt vor Strich. Zwei aufeinanderfolgende Minuszeichen werden zu einem Pluszeichen und liefern uns als Summe die 40.
Multiplikation beim Distributivgesetz
Das Distributivgesetz kann auch eingesetzt werden um eine Klammer zu erzeugen. Eine Summe aus zwei Produkten kann in einen Ausdruck mit Klammer umgeformt werden. Wie immer erst die Formeln und im Anschluss zwei Beispiele.
Formel Distributivgesetz:
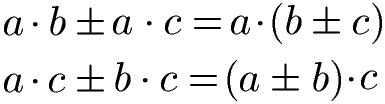
Es handelt sich dabei um die selben Gleichungen wie weiter oben nur das die linke und rechte Seite vertauscht wurden. Mathematisch sind diese jedoch mit den Gleichungen weiter oben identisch.
Distributivgesetz mit natürlichen Zahlen:
Im einfachsten Fall haben wir eine Summe aus zwei Produkten bei denen ein Faktor jeweils gleich ist. In diesem Beispiel kommt die Zahl 3 jeweils vor. Diese 3 kann vor eine Klammer gezogen werden. In der Klammer kommen jeweils die beiden anderen Faktoren vor.
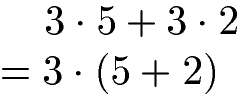
Distributivgesetz mit Dezimalzahlen:
Die Gleichung zum Distributivgesetz funktioniert auch mit negativen Zahlen und Dezimalzahlen (Kommazahlen). Auch in diesem Fall wird die 3 vor die Klammer gezogen.
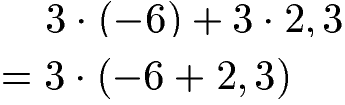
Division beim Distributivgesetz
Um die Grundrechenarten abzuschließen werfen wir noch einen Blick auf das Distributivgesetz für die Division. Die Formel bzw. Gleichung gibt es sowohl für eine Summe (Ergebnis einer Addition) als auch für eine Differenz (Ergebnis einer Subtraktion).
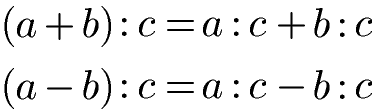
Distributivgesetz Division mit Zahlen:
Ein einfaches Beispiel noch zum Abschluss. Die Summe aus 6 + 4 wird durch die natürliche Zahl 2 geteilt. Mit der Gleichung zum Distributivgesetz der Division kann dies einfach umgeformt werden um die Klammer zu beseitigen.
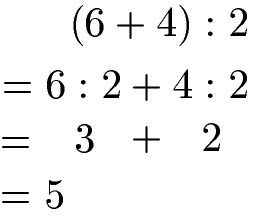
Links:
234 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: