Drachenviereck berechnen und konstruieren

In diesem Artikel geht es um das Drachenviereck. Wir beschäftigen uns mit den Eigenschaften eines Drachenvierecks, wie man dieses berechnen kann und wie man es konstruiert. Dieser Artikel gehört zu unserem Bereich Mathematik Mittelstufe.

In den folgenden Abschnitten befassen wir uns mit dem Drachenviereck. Zuvor solltet ihr jedoch wissen, was ein Viereck überhaupt ist. Aus diesem Grund empfehle ich zunächst den folgenden Artikel zu lesen:

• Rechnen am Viereck

Drachenviereck Eigenschaften

Unter einem Drachenviereck - in der Mathematik auch Deltoid genannt - versteht man ein Viereck mit zwei Paaren gleich langer benachbarter Seiten. Dabei sind die Seiten a und b sowie die Seiten c und d gleich lang. Zwei Winkel werden von der Spiegelachse halbiert. Die Diagonalen stehen zu dem Senkrecht aufeinander. Man kann ein Drachenviereck auf verschiedene Art und Weise konstruieren. Eine Möglichkeit: Die Längen e und f sind gegeben und können gezeichnet werden. Dann werden die Ende der Diagonalen verbunden. Das sieht dann so aus:

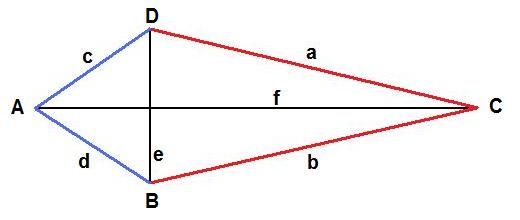
Kommen wir noch zu einigen Formeln. Mit den folgenden Angaben könnt ihr den Flächeninhalt und den Umfang eines Dreiecks berechnen. Beachtet dabei, dass alle Längenangaben in der selben Einheit eingesetzt werden müssen. Im Anschluss an die Formeln findet ihr zu dem noch ein Beispiel.

Drachenviereck Fläche:

Die Fläche eins Drachenvierecks berechnet sich nach der folgenden Formel:

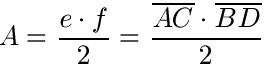
Beispiel: Gegen sie e = 3cm und f = 2cm. Wie groß ist die Fläche des Drachenvierecks?

Lösung: Wir setzen die Angaben in die Formel ein und berechnen die Fläche.

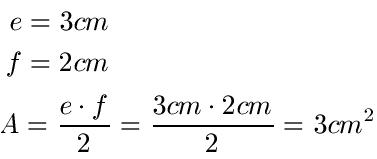
Drachenviereck Umfang:

Kommen wir als nächstes zur Formel für den Umfang des Drachenvierecks:

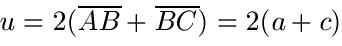
Beispiel: Der Abstand vom Punkt A zum Punkt B beträgt 50cm, der Abstand von B nach C beträgt 1,20m. Berechne den Umfang.

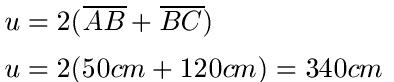
Links:

• Zur Geometrie Übersicht
• Zur Mathematik-Übersicht