Exponentialgleichungen

Mit Exponentialgleichungen befassen wir uns in diesem Artikel. Dabei erklären wir euch, was eine Exponentialgleichung eigentlich ist und wie man sie löst. Dieser Artikel gehört zum Bereich Mathematik.

Zum besseren Einstieg in das Gebiet der Exponentialgleichungen findet ihr hier nun ein paar einleitende Worte: Die meisten von euch mussten sicher schon Gleichungen oder sogar ganze Gleichungssysteme lösen. Dabei hatte man z.B. eine Gleichung der Form 2 + 5x = 0 nach x aufzulösen. Dies wurde durch Addition, Subtraktion, Multiplikation und Division gelöst. Aber angenommen, ihr sollt nun  y = 2^x nach x auflösen. Was dann? Die Lösung lautet: Logarithmus anwenden. Genau darum kümmern wir uns in diesem Abschnitt. Doch zuvor solltet ihr sicherstellen, dass ihr die folgenden Themen kennt. Wer mit diesen noch Probleme hat, folgt den Links. Alle anderen können gleich mit den Exponentialgleichungen loslegen.

• Potenzen
• Gleichungen lösen
• Exponentialfunktionen

Exponentialgleichungen durch Logarithmus lösen

Im nun Folgenden möchten wir euch einige Rechenbeispiele zeigen, wie man durch Einsatz des Logarithmus nach einer Variablen - die im Exponenten steht - auflöst. Unterhalb des jeweiligen Beispiels findet ihr die jeweilige Erklärung.

Exponentialgleichungen Beispiel 1:

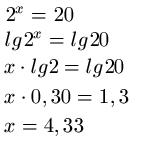
Auf beiden Seiten der Exponentialgleichung wenden wir den dekadischen Logarithmus, auch Zehnerlogarithmus genannt, an. Dadurch können wir das x aus zum Exponenten vor das noch verbleibende lg2 ziehen. Mit dem Taschenrechner berechnen wir lg2 und lg20 und stellen dann die Gleichung nach x um.

Exponentialgleichungen Beispiel 2:

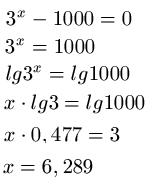
Durch eine Addition mit 1000 schaffen wir die -1000 auf die andere Seite. Dann wenden wir erneut den dekadischen Logarithmus an und ziehen das x vor die lg3. Die Berechnung von lg3 und lg1000 führen wir mit dem Taschenrechner durch und lösen im Anschluss nach x auf.

Exponentialgleichungen Beispiel 3:

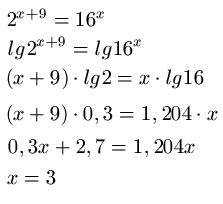
Diese Exponentialgleichung lösen wir ähnlich wie die beiden vorigen: Zunächst wird lg auf beiden Seiten angewendet, wodurch der Exponent nach vorne gezogen werden kann. Die Klammer wird ausmultipliziert und anschließend wie eine normale Gleichung nach x aufgelöst.

Exponentialfunktionen und natürlicher Logarithmus

In diesem Abschnitt soll nun noch gezeigt werden, wie man eine e-Funktion durch Einsatz des natürlichen Logarithmus nach der Unbekannten auflöst. Auch hier bemühen wir uns dies über Beispiele mit Erklärungen zu zeigen.

Exponentialgleichungen Beispiel 4:

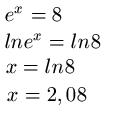
Da wir hier die Basis e ( eulersche Zahl haben ), müssen wir den natürlichen Logarithmus anwenden. Dies führen wir auf beiden Seiten durch und bekommen damit das "e" weg. Durch die Eingabe von ln8 in den Taschenrechner erhalten wir x = 2,08.

Exponentialgleichungen Beispiel 5:

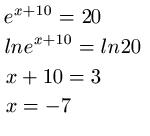
Auch hier wenden wir auf beiden Seiten den natürlichen Logarithmus an und lösen die Gleichung im Anschluss nach x auf.

Links:

• Zur Mathematik-Übersicht