Exponentielles Wachstum / Exponentielle Abnahme

Mit dem exponentiellen Wachstum  und der exponentiellen Abnahme befassen wir uns in diesem Artikel. Wir liefern euch dazu die passenden Formeln und Beispiele. Dieser Artikel gehört zu unserem Bereich Mathematik.

In der Mathematik, Physik und auch in der Biologie kommt so genanntes exponentielles Wachstum und exponentielle Abnahme vor. Genau damit befassen wir uns in diesen Abschnitten. Es ist sinnvoll, dass ihr über einige Vorkenntnisse verfügt. So hilft es zum Beispiel die eulersche Zahl zu kennen und überhaupt zu Wissen, was man unter eine Funktion oder einem Koordinatensystem versteht.

• Koordiantensysteme
• Funktionen
• E-Funktionen

Noch ein Hinweis: Wir sehen uns hier exponentielles Wachstum bzw. Abnahme bei einer E-Funktion an. Natürlich kann eine exponentielle Zunahme auch durch andere Funktionen beschrieben werden. Da die E-Funktion in den Naturwissenschaften und in der Technik häufig vorkommt, beschränken wir uns hier auf diese.

Exponentielles Wachstum / Zunahme

Beginnen wir mit dem exponentiellen Wachstum bzw. exponentiellen Zunahme. Dieses kann zum Beispiel in der Biologie vorkommen, bei der Vermehrung der Population. Dabei steigt die Bevölkerungszahl sehr stark an. Zeichnet man so eine Funktion auf, so sieht dies in etwa so aus. Die folgende Grafik hat jedoch keine Achsenbeschriftung ( dies müsste man für eine Anwendung dann ergänzen ).

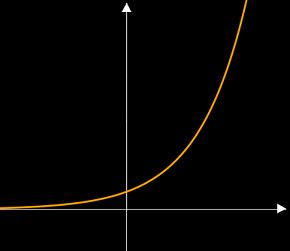
Natürlich kann man dies auch durch eine mathematische Funktion beschreiben. Ein exponentielles Wachstum kann man unter Anderem so darstellen:

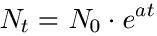
Setzt man nun für N₀ sowie a und t Werte ein, so kann man damit N_t berechnen. Damit kann man nun auch eine Wertetabelle aufbauen und die Funktion in ein Koordinatensystem zeichnen. Exponentielles Wachstum liegt dann vor, wenn a > 0 ist. Wie man dieser Art von Funktion ansehen kann, liegt eine extreme "Steigerungsrate" vor.

Exponentielle Abnahme

Neben der exponentiellen Zunahme gibt es auch noch die exponentielle Abnahme. Diese kommt zum Beispiel in der Physik oder Chemie bei der Zerfallsrate bzw. Halbwertszeit vor. Auch hier zunächst eine Grafik, die eine exponentielle Abnahme zeigt. Eine Achsenbeschriftung muss für Anwendungen natürlich noch hinzugefügt werden.

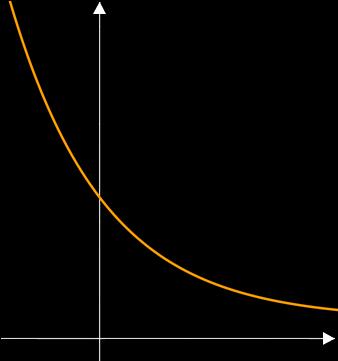
Die Funktion sieht genauso aus wie beim exponentiellen Wachstum:

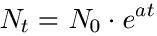
Setzt man nun für N₀ sowie a und t Werte ein, so kann man damit N_t berechnen. Damit kann man nun auch eine Wertetabelle aufbauen und die Funktion in ein Koordinatensystem zeichnen. Exponentielle Abnahme liegt dann vor, wenn a < 0 ist.

Links:

• Zur Mathematik-Übersicht