Hypotenusensatz

Mit dem Hypotenusensatz - besser bekannt unter Satz des Pythagoras - befassen wir uns in diesem Artikel. Was es damit auf sich hat und wie man diesen anwendet, erklären wir in diesem Artikel anhand von Beispielen.Dieser Artikel gehört zu unserem Bereich Mathematik.

Viele kennen den Hypotenusensatz sicher unter einem anderen Namen: Satz des Pythagoras. Mit dem Hypotenusensatz lassen sich Streckenlängen bei einem rechtwinkligen Dreieck berechnen. Um den folgenden Artikel zu verstehen, solltet ihr jedoch einige mathematische Vorkenntnisse haben. Wem die folgenden Themen noch gar nichts sagen, der klickt bitte auf den entsprechenden Artikel und liest sich diesen zunächst einmal durch.

• Dreieck ( Geometrie )
• Rechter Winkel
• Wurzelrechnung

Den Hypotenusensatz anwenden

Den Hypotenusensatz kann man nur an Dreiecken anwenden, welche einen rechten Winkel aufweisen! Schaut euch dazu einmal die folgende Grafik an. Bei dem folgenden Dreieck findet sich links unten ein rechter Winkel.

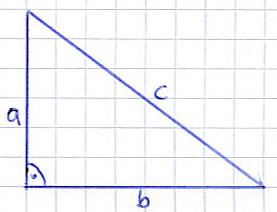
Der rechte Winkel ist Pflicht. Ist dieser nicht vorhanden, ist der Hypotenusensatz nicht anwendbar! Ansonsten lassen sich noch folgende Merkmale feststellen:

• Die Längen a und b bezeichnet man als Katheten. Das sind die beiden Seiten, die direkt an den rechten Winkel angrenzen
• Die Länge c wird als Hypotenuse bezeichnet.

Hypotenusensatz Formel und Beispiele

Der Hypotenusensatz wird dazu benutzt, die dritte Länge eines Dreiecks zu berechnen. Weiß man also zum Beispiel die Länge von a und b, kann man die Länge von c damit berechnen. Die Formel lautet:

• a² + b² = c²
• "a" ist die Länge der Kathete a
• "b" ist die Länge der Kathete b
• "c" ist die Länge der Hypotenuse

Beispiel 1:

• a = 3cm, b = 2cm, c = ?
• Lösung: (3cm)² + (2cm)² = c²
• 9cm² + 4cm² = c²
• 13cm² = c²
• c = 3,6cm

Beispiel 2:

• a = 5cm, c = 10cm, b = ?
• Lösung: (5cm)² + b² = (10cm)²
• 25cm² + b² = 100cm²
• b² = 75cm²
• b = 8.66cm

Ganz wichtig: Den Hypotenusensatz dürft ihr nur anwenden, wenn ein rechter Winkel vorliegt. Die beiden Seiten des Dreiecks, die an diesem liegen, werden mit a und b bezeichnet und die Hypotenuse wird als c bezeichnet. Sind zwei Längen bekannt, werden diese in die Formel eingesetzt und damit die dritte Länge zu berechnen.

Links:

• Übungen: Satz des Pythagoras
• Zur Mathematik-Übersicht