In diesem Abschnitt nutzen wir die Integral-Rechnung zur Bestimmung von Flächen innerhalb von Grenzen. Dabei zeigen wir euch anhand einer Grafik zunächst, was damit gemeint ist und wie man die sogenannten Integrationsgrenzen einsetzt.
Um den folgenden Artikel gut zu verstehen, sind die Grundkenntnisse aus den anderen Bereichen der Integration nötig. Grund: Um die in diesem Abschnitt benutzen Integrale lösen zu können, solltet ihr Wissen, was sich hinter diesem Kapitel der Mathematik verbirgt und wie man eine Stammfunktion bildet. Für alle, die das Vorwissen noch nicht haben, hier noch einmal die Links:
- Grundlagen Integration: Fläche und Summenregel
- Stammfunktion, Potenzregel und Summenregel
- Partielle Integration / Produktintegration
Die Integrationsgrenzen
Zeichnet man eine Funktion, so ergibt das oftmals einen sehr "langen" Verlauf. Jetzt will man natürlich nicht die komplette Fläche unter einer Funktion erhalten, die ist oftmals unendlich. Sondern nur die Fläche in einem gewissen Abschnitt. Deshalb setzt man so genannte Integrationsgrenzen. Schaut euch dazu erst einmal die folgende Grafik an:
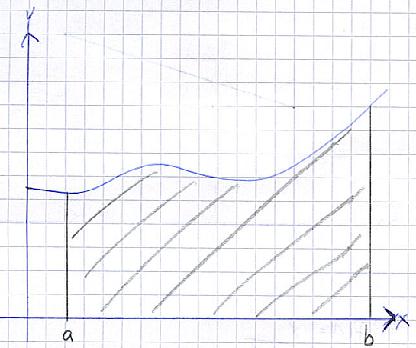
Die Integrationsgrenzen werden meist mit a und b bezeichnet, wobei a die "untere" Integrationsgrenze und "b" die "obere" Integrationsgrenze bezeichnen. Heißt auf gut Deutsch: Die Fläche unter der Funktion von a bis b ist gesucht. Um diese zu bekommen müsst ihr wie folgt vorgehen:
- Integriert die Funktion mittels der Integrationsregeln
- Die Konstante "C" wird 0 gesetzt, sprich sie verschwindet
- Die Funktion mit oberer Grenze minus Funktion mit unterer Grenze berechnen
Beispiel 1: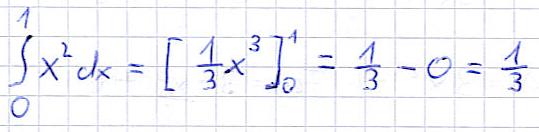
Erklärungen: Die Funktion wird zunächst integriert. Die Stammfunktion wird in Klammern gesetzt und die Integrationsgrenzen werden an diese angetragen. Danach wird die Funktion ausgerechnet mit dem oberen Grenzwert: Setzt man die 1 in die Gleichung ein, erhält man ein Drittel. Danach wird ein minus "-" gesetzt". Hinter diesem wird der Funktionswert für die untere Grenze gebildet. Setzt man die 0 ein, ergibt sich eine Null. Dies ergibt ein Drittel als Gesamtergebnis.
Beispiel 2: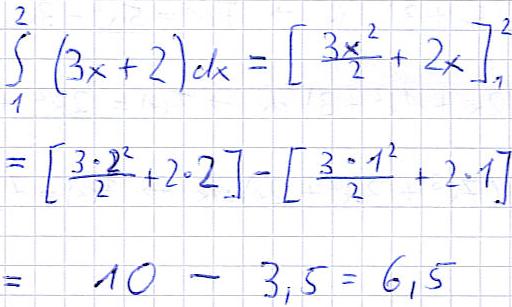
Erklärungen: Auch hier wurde erst integriert und die Grenzen angetragen. Dann wurde der Wert für die obere Grenze eingesetzt und ausgerechnet und davon das Ergebnis der Funktion mit der unteren Grenze abgezogen.
Links:
191 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
