Integrieren Grundlagen: Fläche und Summenregel

In diesem Artikel behandeln wird die Grundlagen der Integral-Rechnung um Flächen zu berechnen. Dabei zeigen wir euch anhand eines Beispiels, wie man von einer Summenregel auf das Integrieren kommt.

Um die Grundlagen der Integral-Rechnung zu verstehen, solltet ihr Basiswissen zum Berechnen von Flächen haben und am Besten auch schon über das Differenzieren einiges Wissen. Wer in diesen Themen noch Lücken hat, sollte den folgenden Links folgen. Alle anderen können dies überspringen.

• Fläche Rechteck und Kreis
• Ableitung von Funktionen

Obersumme und Untersumme

Im Folgenden zeigen wir euch, was es mit der Summenregel auf sich hat. Ziel ist es, die Fläche unter einer Funktion  zu berechnen. Wir beginnen dabei mit der Untersumme. Schaut euch einmal die folgende Grafik an:

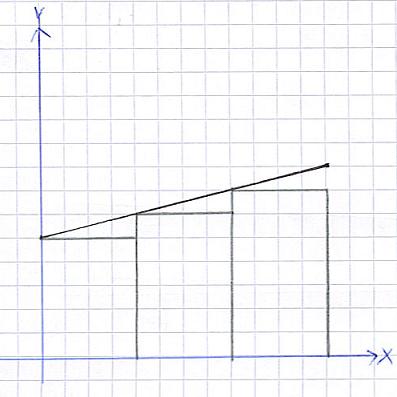
Die Untersumme:

In schwarz wird die Funktion dargestellt. Um die Fläche unter dieser zu berechnen, wurden Rechtecke eingezeichnet ( mit einer Breite von 2cm ). Wir ihr sicher wisst: Die Fläche eines Rechtecks berechnet sich aus Länge mal Breite. Man kann somit die Fläche aller Rechtecke ausrechnen und zusammen addieren. So erhält man die Fläche unter einer Funktion. Allerdings entsteht hier ein kleiner Fehler: Wie ihr sehen könnt, fehlt ein kleines Stück Fläche zwischen den Rechtecken und der Funktion. Es "fehlt" also Fläche. Dies war die Untersumme.

Die Obersumme:

Als nächstes beschäftigen wir uns mit der Obersumme. Die Vorgehensweise ist sehr ähnlich zur Untersumme. Nur hier werden die Rechtecke etwas größer angesetzt. Werft aber erst einmal einen Blick auf die folgende Grafik:

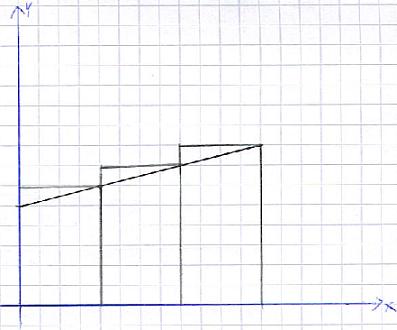
Es werden also erneut Rechtecke erzeugt. Deren Flächeninhalte ist ebenfalls Länge mal Breite. Und die einzelnen Rechtecke werden zu einer Gesamtsumme addiert. Nur hier ist die Summe größer als die eigentliche Fläche. Somit hat die Untersumme eine Fläche geliefert, die zu klein ist. Die Obersumme hingegen hat eine Fläche geliefert, die zu groß ist.

Exakte Fläche bestimmen

Sowohl die Obersumme, als auch die Untersumme haben ein "etwas" falsches Ergebnis geliefert. Das korrekte Ergebnis liegt irgendwo dazwischen. Aber wie bekommt man das richtige Ergebnis raus? Die Antwort ist eigentlich recht einfach: Es müssen mehr Rechtecke eingesetzt werden. Je mehr Rechtecke ihr habt, desto kleiner sind die fehlenden Flächen bzw. die Flächen, die zu groß sind. Ihr nähert euch damit dem "realen" Verlauf der Funktion viel besser an. Habt ihr praktisch unendlich viele Rechtecke, erhaltet ihr das Integral!

Allerdings ist es viel zu umständlich, eine große Anzahl an Rechtecken ein zu zeichnen, deren Fläche zu berechnen und das Ganze auf zu summieren. Aus diesem Grund, haben Mathematiker sich Gedanken gemacht, wie man dies einfacher lösen kann. Die Lösung lautet: Mittels einiger Regeln die Funktion integrieren und dadurch die Fläche zu erhalten. Wie diese Regeln funktionieren, lernt ihr ab dem nächsten Abschnitt.

Links:

• Elementare Integrationsregeln
• Zur Integral-Übersicht
• Zur Mathematik-Übersicht