Inverse Funktion bilden und ableiten

In diesem Artikel befassen wir uns mit der inversen Funktion und deren Ableitung. Dabei werden auch verschiedene Aufgaben vorgerechnet. Dieser Artikel gehört zu unserem Bereich Mathematik.

Bevor wir uns um die inverse Funktion kümmern, solltet ihr kurz nachsehen ob euch die folgenden Themen schon etwas sagen. Ist das nicht so, dann lest bitte erst einmal die gleich verlinkten Inhalte durch. Denn wer diese bereits kennt tut sich wesentlich leichter mit dem Bilden der inversen Funktion sowie deren Ableitung.

• Lineare Funktion
• Quadratische Funktion
• Faktorregel + Summenregel

Inverse Funktion berechnen

In der Mathematik hat man sehr oft Funktionen der Art y = f(x), also zum Beispiel y = 3x + 2 oder y = 5x + 5.  Löst man nun diese Funktionen nach der Variablen "x" auf und vertauscht anschließend x und y, dann erhält man die Funktionsgleichung der inversen Funktion. Diese inverse Funktion wird oft mit f^-1 bezeichnet. Leider ist es so, dass dies nicht immer möglich ist. Kommen wir zu einem "Schlachtplan".

Allgemeine Vorgehensweise:

• Die Funktionsgleichung y = f(x) lösen wir nach der Variablen x auf.
• Im Anschluss vertauschen wir x und y.

Beispiel 1: Lineare Funktion

Gegeben sei eine Gerade mit y = 2x + 1. Ziel ist es die inverse Funktion zu bestimmen. Dazu lösen wir diese Gleichung nach x auf und vertauschen im Anschluss x und y. Bei dieser Funktion ist es möglich die inverse Funktion zu berechnen, da jedem X-Wert ein  Y-Wert zugeordnet werden kann. Wir erhalten dadurch y = 0,5x - 0,5. Hier die komplette Rechnung:

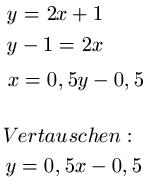
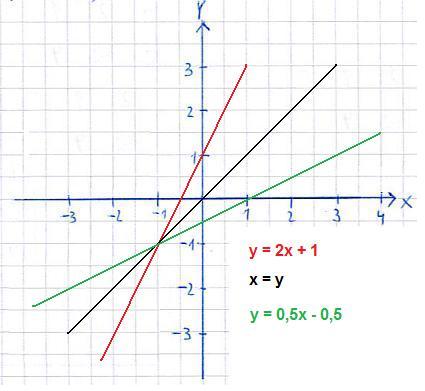
Inverse Funktion grafisch:

Nachdem wir nun ein Beispiel gerechnet haben sehen wir uns die inverse Funktion einmal grafisch in einem Koordinatensystem an. In rot seht ihr die Startfunktion y = 2x + 1 und in grün die inverse Funktion y = 0,5x - 0,5.  Nun zeichnen wir uns noch mit x = y die Winkelhalbierende im 1. und 3. Quadranten des Koordinatensystems ein. Spiegelt man nun einen Punkt der roten Gerade an der Winkelhalbierenden erhält man einen Punkt auf der grünen Geraden. Damit haben wir den Zusammenhang zwischen der Ausgangsfunktion und ihrer Inversen gefunden.

Beispiel 2: Lineare Funktion

Als nächstes sehen wir uns die ebenfalls lineare Funktion y = 3x - 5 an. Auch hier bilden wir die inverse Funktion, indem wir zunächst nach x auflösen und im Anschluss x und y vertauschen. Und auch hier handelt es sich um eine lineare Funktion, daher ist das Bilden der inversen Funktion auch möglich.

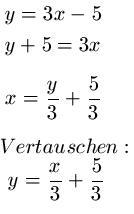
Beispiel 3: Quadratische Funktion & Probleme

Bei einer quadratischen Funktion wie zum Beispiel y = x² tritt ein Problem auf. Hier liegt keine eindeutige Zuordnung vor, denn einem y-Wert sind zwei x-Werte zugeordnet. So erhält man y = 4 sowohl mit x = 2 als auch mit x = -2. Oder y = 9 erhält man sowohl mit x = 3 als auch mit x = -3.  Um hier dennoch die inverse Funktion bilden zu können, muss man zwei verschiedene Fälle unterscheiden können. So sehen wir uns einmal den Bereich für positive x-Werte und einmal den Bereich für negative x-Werte an. Dadurch entstehen zwei inverse Funktionen. Das sieht dann so aus:

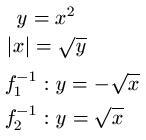
Beispiel 4: E-Funktion

Sehen wir uns als nächstes eine E-Funktion an. Dabei soll die inverse Funktion von y = e^x gebildet werden. Durch Einsatz des natürlichen Logarithmus erhalten wir zunächst x = ln(y). Nun vertauschen wir wieder x und y und erhalten als inverse Funktion y = ln(x).

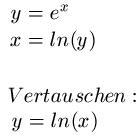
Ableitung der inversen Funktion

Anhand von zwei wirklich typischen Beispielen möchte ich euch gleich die Ableitung der inversen Funktion zeigen. Zunächst jedoch die allgemeine Gleichung und einen Plan zur Vorgehensweise.

Gleichung Ableitung inverse Funktion:

Liegt eine umkehrbare Funktion der Form y = f(x) vor und ist zugleich x = g(y) die nach x umgeformte Darstellung dieser Funktion dann gilt:

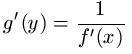
Der Nenner - also f'(x) darf hier natürlich nicht Null werden. Darüber hinaus muss - wie bereits weiter oben geschrieben - die Funktion überhaupt umkehrbar sein.

Allgemeine Vorgehensweise:

1. Wir schreiben uns y = f(x) auf
2. Wir leiten f(x) ab und erhalten y' = f'(x)
3. Wir stellen f(x) nach x um
4. Wir setzen in die Gleichung f'(x) ein
5. Wir ersetzen den Ausdruck von f'(x) durch y
6. Wir vertauschen x und y

Inverse Funktion ableiten Beispiele

Die eben gezeigte Gleichung sowie die allgemeine Vorgehensweise soll nun auf Beispiele angewendet werden. Zur besseren Übersicht schreibe ich vor jede Berechnung noch den jeweiligen Schritt aus der "allgemeinen Vorgehensweise". Ich empfehle neben dem PC auf einem Stück Papier noch einmal die Aufgabe selbst mitzurechnen.

Beispiel 1:

Gegeben sei die Funktion y = f(x) = e^x. Gesucht ist nun die Ableitung der inversen Funktion. Wir schreiben für den ersten Schritt die Aufgabe ab und leiten die Funktion für den zweiten Schritt ab. Da die Ableitung von e^x wieder e^x ist sollten hier keine Verständnisprobleme auftreten. Im dritten Schritt lösen wie y = e^x nach x auf. Dazu benötigen wir den natürlichen Logarithmus, den wir auf beide Seiten anwenden. Wir erhalten dadurch x = ln(y).

Beim vierten Schritt setzen wir in die oben genannte Gleichung für f'(x) nun e^x ein, so wie wir dies im zweiten Schritt berechnet haben. Wir erhalten dadurch g'(y) = 1 durch e^x. Aus der Aufgabenstellung wissen wir, dass y = e^x ist. Somit können wir in Schritt 5 für e^x nun einfach y einsetzen. Im letzten Schritt tauschen wir einfach noch y durch x aus und erhalten dadurch die Ableitung der inversen Funktion. Das sieht dann also so aus:

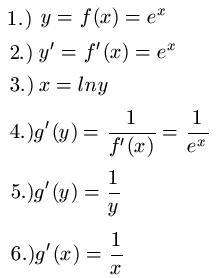
Beispiel 2:

Gegeben sei die Funktion y = f(x) = tan x . Gesucht ist nun die Ableitung der inversen Funktion. Aus der Formelsammlung entnehmen wir die Ableitung zu f'(x) = tan²x + 1. Für den dritten Punkt stellen wir y = tan x nach x um und erhalten x = arctan(y). Mit den gewonnen Informationen gehen wir bei Punkt 4 in die oben genannte Formel.  Für den Punkt 5.) muss man wissen, dass wir am Anfang y = tan x da stehen hatten und wir damit aus tan²x nun y² machen können. Im letzten Schritt tauschen wir y durch x aus.

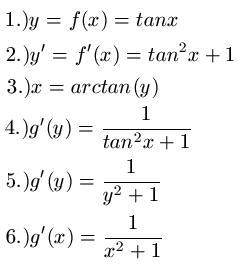
Links:

• Umkehrfunktion Aufgaben / Übungen
• Zur Mathematik-Übersicht