Das Kommutativgesetz für die Addition, Subtraktion, Multiplikation und Division wird hier erklärt. Ihr lernt dabei in welchen Fällen das Kommutativgesetz eingesetzt werden darf und welche Fehler ihr nicht machen dürft. Dieser Artikel gehört zum Bereich Mathematik.
Was ist das Kommutativgesetz? Zunächst eine Erklärung bzw. Definition zum Kommutativgesetz.
Hinweis:
Das Kommutativgesetz sagt aus, dass bei einer Addition oder Multiplikation die Zahlen vertauscht werden dürfen ohne das sich das Ergebnis der Berechnung ändert. Daher wird das Kommutativgesetz auch Vertauschungsgesetz genannt.
Kommutativgesetz Addition:
Eine Addition besteht aus mindestens zwei Summanden und einer Summe. Die nächste Grafik zeigt kurz die wichtigen Begriffe zur Addition.

Das Kommutativgesetz der Addition sagt nun aus, dass man die Reihenfolge der Summanden verändern darf ohne das sich die Summe ändert. Die Formel oder Gleichung zum Kommutativgesetz der Addition wird so angegeben:
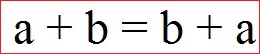
Kommutativgesetz Addition Beispiele:
Die Reihenfolge der Zahlen beim Addieren spielt keine Rolle. Ob 1 + 4 addiert wird oder 4 + 1 spielt keine Rolle, denn die Summe ist immer 5.
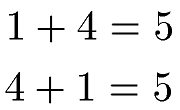
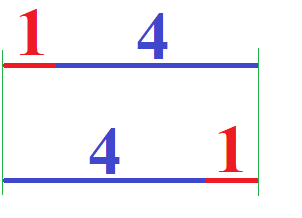
Dies kann man sich auch grafisch veranschaulichen. Ob erst 1 Meter gefahren wird und im Anschluss 4 Meter oder erst 4 Meter und danach 1 Meter spielt keine Rolle. Die Strecke bleibt gleich lang.
Das Kommutativgesetz der Addition funktioniert auch für negative Zahlen. Eine negative Zahl (-3) und eine positive Zahl (+4) werden addiert. Wichtig ist den Unterschied zwischen Rechenzeichen und Vorzeichen zu beachten. Da die Addition kommutativ ist lautet das Ergebnis jeweils 1.
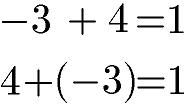
Bei einer Addition mit 3 Summanden oder mehr darf ebenfalls vertauscht werden. Ausführlich werden 3 Summanden noch beim Assoziativgesetz behandelt.
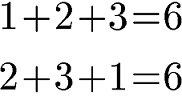
Kommutativgesetz Subtraktion
Das Kommutativgesetz gilt nicht für die Subtraktion! Dennoch lässt sich beim Vertauschen etwas interessantes feststellen. Zunächst jedoch erst einmal die wichtigen Begriffe zur Subtraktion: Minuend, Subtrahend und Differenz.

Die nächste Formel bzw. Ungleichung zeigt, dass man Minuend und Subtrahend nicht vertauschen darf.
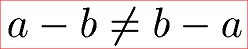
Kommutativgesetz Subtraktion Beispiele:
Werden Minuend und Subtrahend bei der Subtraktion vertauscht ist die Differenz unterschiedlich. Das Kommutativgesetz gilt daher nicht für die Subtraktion!
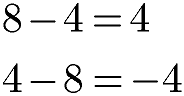
Eine Auffälligkeit gibt es jedoch bei der Differenz. Hier ändert sich nur das Vorzeichen. Aus +4 wird -4. Im nächsten Beispiel wird bei der Differenz durch das Vertauschen aus +2 einfach -2.
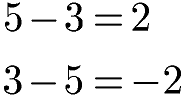
Das Vertauschen von Minuend und Subtrahend ändert bei der Differenz das Vorzeichen. Da die Differenz dennoch verschieden ist gilt das Kommutativgesetz für die Subtraktion nicht.
Kommutativgesetz der Multiplikation
Das Kommutativgesetz der Multiplikation besagt, dass bei einer Multiplikation die Reihenfolge der Zahlen vertauscht werden darf. Auch hier zunächst ein kurzer Blick auf die Begriffe Faktor und Produkt.

Bei der Multiplikation darf die Reihenfolge der Faktoren vertauscht werden ohne das sich das Produkt verändert. Die allgemeine Formel oder Gleichung zum Kommutativgesetz der Multiplikation lautet:
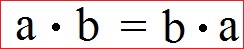
Es spielt keine Rolle, ob es sich bei den Faktoren um natürliche Zahlen, ganze Zahlen, negative Zahlen, Brüche oder Dezimalzahlen handelt. Es folgen noch einige Rechenbeispiele und eine grafische Veranschaulichung.
Kommutativgesetz Multiplikation Beispiele:
Multipliziert werden die Faktoren 2 und 4. In beiden Fällen ist das Produkt 8.
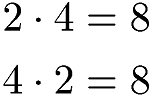
Ein praktisches Beispiel wäre die Fläche von einem Raum. Nehmen wir einen Raum mit 2 Meter Breite und 4 Meter Länge. Damit hätte der Raum eine Fläche von 8 Quadratmeter. Tauscht man Länge und Breite bleibt die Fläche jedoch bei 8 Quadratmeter.
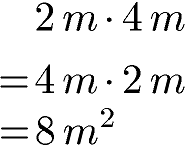
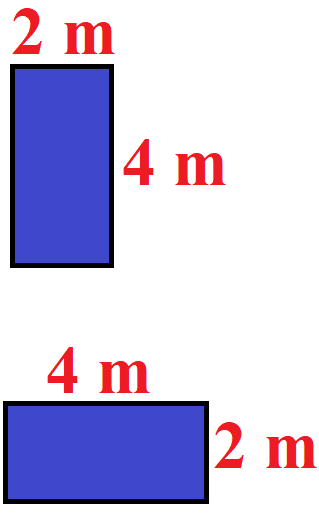
Die kann man sich auch grafisch sehr schön ansehen. Die blaue Fläche ist in beiden Fällen gleich groß.
Kommutativgesetz Division
Das Kommutativgesetz gilt nicht für die Division! Zunächst wie auch bei den Grundrechenarten die Fachbegriffe zur Division.
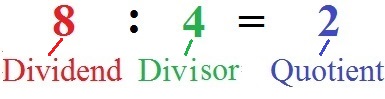
Die nächste Ungleichung zeigt, dass das Kommutativgesetz bei der Division nicht gilt:
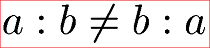
Kommutativgesetz Division Beispiele:
Zum besseren Verständnis werden für ein Beispiel Dividend und Divisor vertauscht. Wie klar zu sehen ist unterscheiden sich die Quotienten.
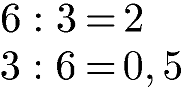
Eine alternative Schreibweise für eine Division ist die Darstellung als Bruch. Das letzte Beispiel kann auch in Form von Brüchen geschrieben werden.
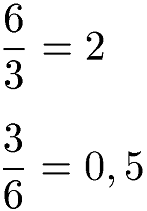
Links:
105 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: