Kongruenz / Kongruenzsätze

Mit der Kongruenz bzw. mit den Kongruenzsätzen befassen wir uns in diesem Artikel. Dabei werden auch entsprechende Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik Mittelstufe.

Mit der Kongruenz bzw. den Kongruenzsätzen befassen wir uns in diesem Artikel. Als Beispiel dient dazu ein Dreieck. Aus diesem Grund empfehle ich zunächst den folgenden Artikel zu lesen:

• Dreieck

Was versteht man unter Kongruent?

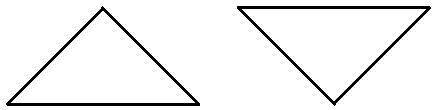
Stellt sich zunächst die Frage, was man unter Kongruent überhaupt versteht. In der Geometrie sind zwei Figuren kongruent, wenn sie durch eine Kongruenzabbildung ineinander überführt werden können. Kongruenzabbildungen sind Parallelverschiebung, Drehung, Spiegelung und die Verknüpfungen dieser Abbildung. Die folgende Grafik zeigt zwei Dreiecke, die zueinander kongruent sind. Denn man kann das eine Dreieck in das andere durch Drehung überführen.

Kongruenzsätze SSS, SWS, WSW und SSW

Woran erkennt man denn nun,dass zwei Dreiecke kongruent zueinander sind? Die Antwort darauf liefern die Kongruenzsätze sss, sws, wsw und ssw. Diese vier Kongruenzsätze sehen wir uns nun an.

• Kongruenzsatz sss: Zwei Dreiecke sind zueinander kongruent, wenn sie in allen drei Seiten übereinstimmen.
• Kongruenzsatz sws: Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen.
• Kongruenzsatz wsw: Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Winkeln und der eingeschlossenen Seite übereinstimmen.
• Kongruenzsatz ssw: Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel übereinstimmen.

Links:

• Zur Geometrie Übersicht
• Zur Mathematik-Übersicht