Lineare Abhängigkeit von 3 Vektoren

Mit der linearen Abhängigkeit von 3 Vektoren befassen wir uns in diesem Artikel. Dabei geht es darum, was man unter lineare Abhängigkeit versteht und es wird anhand von Beispielen gezeigt, ob drei Vektoren linear abhängig sind oder eben nicht. Dieser Artikel gehört zu unserem Bereich Mathematik.

Bevor wir mit der linearen Abhängigkeit von drei Vektoren beginnen, solltet ihr eure Vorkenntnisse kurz checken: Wem die folgenden Themen noch gar nichts sagen, der möge diese bitte erst nachlesen. Alle anderen können gleich mit dem nächsten Abschnitt weiter machen.

• Parallelität, Komplanarität und Kollinearität
• Lineare Abhängigkeit bei 2 Vektoren
• Determinante berechnen

Beispiele zu lineare Abhängigkeit von drei Vektoren

Erst einmal ein kurzer Hinweis: Wer noch nicht weiß, was es mit linearer Abhängigkeit auf sich hat und auch noch keinen Schimmer davon hat, was eine Determinante ist, dem empfehle ich zunächst die weiter oben verlinkten Inhalte anzusehen. Denn nur so lassen sich die folgenden Inhalte überhaupt verstehen.

In den folgenden Beispielen sehen wir uns nun an, ob 3 Vektoren linear abhängig sind oder eben nicht. Dabei gilt: Ist die Determinante D = 0, so sind die Vektoren linear abhängig.  In diesem Fall sind die Vektoren komplanar, dass heißt sie liegen in einer gemeinsamen Ebene.

Beispiel 1:

Gegeben sind drei andere Vektoren. Die Frage lautet nun: Sind diese linear abhängig oder nicht? Dazu berechnen wir deren Determinante ( Artikeltipp: Determinante berechnen ).

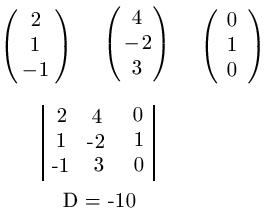
Die Determinante berechnet sich zu D = -10. Die Vektoren sind linear nicht abhängig ( = unabhängig ).

Links:

• Zur Vektor-Übersicht
• Zur Mathematik-Übersicht