Multiplizieren bzw. Multiplikation (Mathe)

Was ist multiplizieren bzw. was bedeutet multiplizieren? Wie multipliziert man kleine Zahlen, etwas größere Zahlen und ganz große Zahlen? Dies lernst du in diesem Artikel. Die Inhalte gibt es als Video und als Text. Außerdem gibt es am Ende des Artikels noch Übungsaufgaben mit Lösungen.

Eine Multiplikation erkennt man an einem Malzeichen. In Büchern oder im Internet wird als Malzeichen entweder ein · oder * genutzt. Eine Multiplikation ist eine Abkürzung für eine Addition.

Beispiel 1: Kleine Multiplikation

Die Multiplikation 2 · 8 bedeutet nichts anderes als das man 2 Mal die Zahl 8 hinschreibt und ein Pluszeichen dazwischen schreibt.

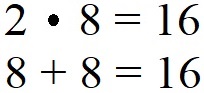
Beispiel 2: Kleine Multiplikation

Die Multiplikation 3 · 4 bedeutet nichts anderes als das man 3 Mal die Zahl 4 hinschreibt und ein Pluszeichen dazwischen schreibt.

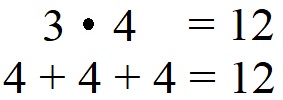
Hinweis: Die beiden Zahlen welche multipliziert werden nennt man Faktoren. Das Ergebnis der Multiplikation wird als Produkt bezeichnet.

Multiplikation Gesetz und halbschriftlich

Bei der Multiplikation spielt es keine Rolle in welcher Reihenfolge die Zahlen stehen. Ob ich 2 · 8 rechne oder 8 · 2 ausrechne spielt für das Ergebnis keine Rolle. In beiden Fällen ist 16 das Ergebnis der Rechnung.

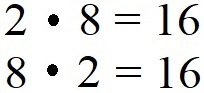
Mehr dazu findest du unter Kommutativgesetz der Multiplikation.

Halbschriftliche Multiplikation:

Werden die Zahlen für die Multiplikation etwas größer, schafft man dies oft nicht mehr im Kopf auszurechnen. Ist eine der beiden Zahlen zweistellig und die andere einstellig verwendet man oftmals die halbschriftliche Multiplikation.

Beispiel 3: Halbschriftliche Multiplikation

Berechnet werden soll 8 · 23. Für die Berechnung zerlegen wir die 23 in 20 und 3. Beides multiplizieren wir mit der 8. Die Produkte der beiden Multiplikationen sind 160 und 24. Wir addieren diese und erhalten als Gesamtergebnis 184.

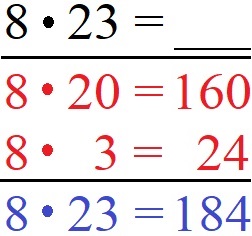
Multiplikation schriftlich mit Beispielen

Werden die Zahlen bei der Multiplikation noch größer, verwendet man die schriftliche Multiplikation. Bei dieser zieht man unter die Malaufgabe einen Strich. Unter diesen Strich kommt die Lösung der Aufgabe.

Beispiel 4: Schriftliche Multiplikation ohne Übertrag

Berechnet werden soll 2134 · 2. Die kleinere Zahl schreiben wir nach hinten, dies vereinfacht die Berechnung. Wir multiplizieren die 2 mit jeder Stelle der ersten Zahl:

• 2 · 4 = 8
• 2 · 3 = 6
• 2 · 1 = 2
• 2 · 2 = 4

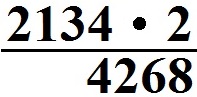
Beispiel 5: Schriftliche Multiplikation mit Übertrag

Berechnet werden soll 4 · 6718. Um die Aufgabe einfacher ausrechnen zu können schreiben wir die Aufgabe jedoch in der Form 6718 · 4. Bei der Berechnung des Produkts entsteht ein Übertrag. Ein Übertrag entsteht wenn eine Multiplikation größer als 9 wird. Schaut einfach mal auf die Berechnung:

• 4 · 8 = 32.
  • Wir schreiben 2 und merken uns 3 als Übertrag.
• 4 · 1 = 4. Mit Übertrag 4 + 3 = 7
  • Wir schreiben 7 in das Ergebnis.
• 4 · 7 = 28.
  • Wir schreiben 8 und merken und 2 als Übertrag.
• 4 · 6 = 24. Mit Übertrag 24 + 2 = 26.
  • Wir schreiben die 6 und merken und 2 als Übertrag.
• Keine weitere Stelle vorhanden. Daher noch die 2 vom Übertrag schreiben.

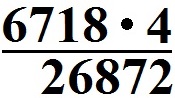
Beispiel 6: Schriftliche Multiplikation zweistellige Zahl

Berechnet werden soll 3410 · 12. Wie man hier sehen kann ist die zweite Zahl zweistellig. Der Rechenweg wird dadurch etwas umfangreicher. Seht erst einmal auf die Lösung der Aufgabe. Unterhalb folgt der Rechenweg.

Rechenweg:

• Wir multiplizieren die 1 mit 3410, ergibt 3410. Diese 3410 schreiben wir so, dass die 0 unter der 1 weiter oben steht.
• Wir multiplizieren die 2 mit 3410, ergibt 6820. Diese 6820 schreiben wir so, dass die 0 unter der 2 weiter oben steht.
• Wir addieren die beiden Ergebnisse schriftlich und erhalten 40920 als Produkt.

Weitere Inhalte:

• Übungsaufgaben Multiplikation
• Schriftliche Multiplikation
• Mathematik - Übersicht