Natürliche Zahlen verstehen ▷ Definition, Beispiele und mehr

Natürliche Zahlen sehen wir uns hier mit Definition, Zeichen und Beispielen an. Außerdem sehen wir uns den Unterschied zu ganzen Zahlen sowie rationalen Zahlen an. Dabei lernt ihr auch was nicht natürliche Zahlen sind. Die Inhalte liegen als Text und als Video vor.

Was sind natürliche Zahlen? Dazu sehen wir uns erst einmal eine Definition an:

Hinweis:
Natürliche Zahlen sind Zahlen, welche zum Zählen verwendet werden können. Ob die Null (0) ebenfalls zu den natürlichen Zahlen gezählt wird, hängt von der Definition ab. Das Zeichen für natürliche Zahlen ist ein N mit einem doppelten Strich.

Falls man die natürlichen Zahlen ohne 0 angibt, sieht die Menge wie folgt aus:

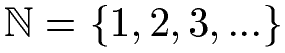
Die natürlichen Zahlen mit 0 werden hingegen so angegeben:

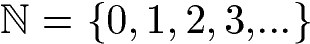
Alle anderen Zahlen sind nicht natürlich. Beispiele dazu findet ihr ab dem nächsten Abschnitt.

Beispiele: Natürliche Zahlen und ganze Zahlen

Natürliche Zahlen sind die Zahlen, welche ich mit den Fingern abzählen kann. Alle anderen Zahlen gehören dazu nicht. Daher werfen wir als nächstes einen Blick auf die ganzen Zahlen. Die ganzen Zahlen sind alle natürlichen Zahlen und genau diese Zahlen auch mit einem Minuszeichen davor.

Beispiele: In der nächsten Grafik sind die grün eingekreisten Zahlen natürlich. Die rot eingekreisten Zahlen sind hingegen nicht natürlich. Alle Zahlen in der Grafik sind jedoch ganze Zahlen.

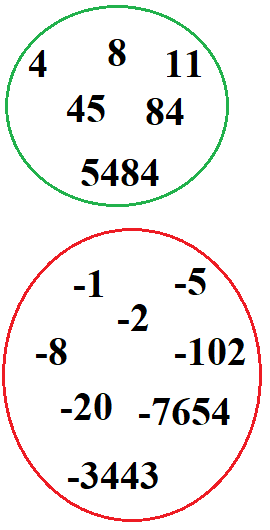
Im nächsten Abschnitt geht es um unnatürliche Zahlen.

Welche Zahlen sind nicht natürlich?

Sehen wir uns noch einige weitere Beispiele zu unnatürlichen Zahlen an. Dazu gehören:

• Negative Zahlen sind nicht natürlich.
• Zahlen die nur mit einem Komma dargestellt werden können sind nicht natürlich.
• Viele Brüche (nicht alle), welche ausgerechnet eine Kommazahl ergeben sind ebenfalls unnatürlich. Beispiele weiter unten.
• Viele Wurzeln (nicht alle) ergeben ausgerechnet meistens nicht natürliche Zahlen.

Hier einige Beispiele für nicht natürliche Zahlen:

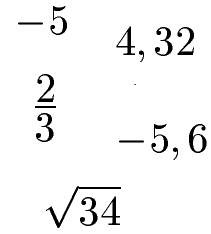
Hier wird auch klar warum 0 die kleinste natürliche Zahl ist: Zahlen kleiner als Null sind negativ und negative Zahlen sind nicht natürlich.

Brüche und natürliche Zahlen

Wie hängen Brüche und natürliche Zahlen zusammen? Nun, ein Bruch ist nichts anderes als eine Division. Zum Beispiel kann die Rechenaufgabe 6 : 2 = 3 auch in Form eines Bruchs geschrieben und ausgerechnet werden.

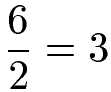
Das Ergebnis des letzten Bruchs ist die Zahl 3, also eine natürliche Zahl. Im nächsten Beispiel entsteht ebenfalls eine natürliche Zahl, wenn der Bruch ausgerechnet wird.

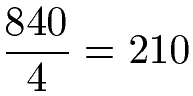
Wer Probleme in der Berechnung hat, kann die letzte Aufgabe auch mit der schriftlichen Division lösen.

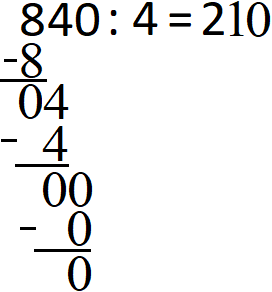
Oftmals kommt eine unnatürliche Zahl bei der Berechnung von einem Bruch raus. Zu sehen im nächsten Beispiel:

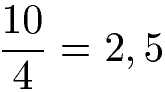
Wir lernen: Nicht jeder Bruch ergibt ausgerechnet eine natürliche Zahl.

Links:

• Natürliche Zahlen Übungen
• Zahlenarten
• Mathematik Übersicht