Potenzen addieren ▷ Beispiele und Erklärungen

Die Addition von Potenzen sehen wir uns hier an. Du lernst mit einfachen Beispielen was man unter Basis und Exponent versteht. Den Umgang mit gleichen oder verschiedenen Basen und Exponenten zeige ich dir ebenfalls. Diese Mathematik-Inhalte liegen als Text und als Video vor.

Um die Addition von Potenzen zu verstehen, solltest du drei wichtige Begriffe kennen: Basis, Exponent und Potenzwert. Ein Beispiel:

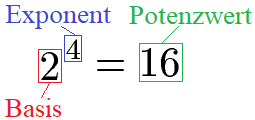
Eine Potenz besteht aus Basis und dem Exponent. Wird die Potenz ausgerechnet, ist das Ergebnis der Potenzwert. Solltest du noch nicht wissen wie man eine solche Potenz berechnet, lernst du dies im Artikel Potenzen. Werfen wir nun einen Blick auf die Regeln zur Addition von Potenzen.

Potenzen addieren: Gleiche Basis und gleicher Exponent

Bei gleicher Basis und gleichem Exponenten können zwei Potenzen einfach addiert werden. Dazu werden die Koeffizienten (hier a und b) einfach addiert während der restliche Teil unverändert bleibt. Die allgemeine Schreibweise lautet:

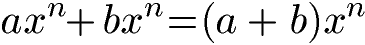
Als Beispiel sollen zwei Potenzen addiert werden bei denen die Basis (x oder z) und der Exponent (2 oder 4) gleich sind.

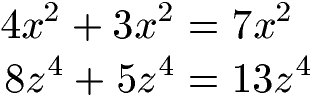
Die Addition von Potenten funktioniert auch bei mehr als 2 Summanden. Im nächsten Beispiel liegen drei Summanden mit gleicher Basis (a) und gleichem Exponenten (2) vor. Auch hier können die Koeffizienten einfach addiert werden.

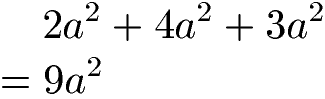
Bei gleicher Basis und gleichem Exponenten lässt sich sehr einfach eine Potenz addieren. Unterschiedliche Basen und Exponenten bringen jedoch Probleme in der Berechnung. Dies sehen wir uns gleich an.

Addition von Potenzen mit unterschiedlichen Exponenten

Die Addition von Potenzen mit unterschiedlichen Exponenten kann nicht mit einer allgemeinen Schreibweise dargestellt werden. Bei gleicher Basis aber unterschiedlichem Exponenten kann daher keine Gleichung für die Umformung angeben werden.

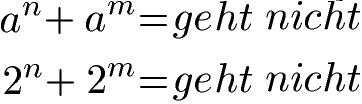
Die Addition von Potenzen mit gleicher Basis aber verschiedenen Exponenten kann in einigen Fällen dennoch durchgeführt werden. Dies ist möglich wenn keine Variablen, sondern ausschließlich Zahlen vorliegen.

Im nächsten Beispiel werden zwei Potenzen mit unterschiedlichem Exponenten addiert. Dazu wird jede Potenz einzeln ausgerechnet und im Anschluss werden die beiden Potenzwerte addiert.

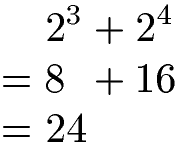
Hinweis: In der Mathematik wird zuerst eine Potenz berechnet und erst im Anschluss Punkt vor Strich eingehalten. Aus diesem Grund wurden im letzten Beispiel erst die Potenzen 2³ und 2⁴ ausgerechnet und im Anschluss addiert.

Potenzen addieren mit unterschiedlicher Basis

Die Addition von Potenzen mit unterschiedlicher Basis kann nicht mit einer allgemeinen Schreibweise dargestellt werden. Bei ungleicher Basis aber gleichem Exponenten kann daher keine Gleichung für die Umformung angeben werden.

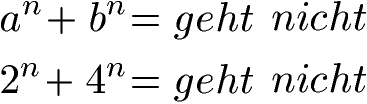
Die Addition von Potenzen mit ungleicher Basis aber gleichem Exponenten kann in einigen Fällen dennoch durchgeführt werden. Dies ist möglich wenn keine Variablen (Buchstaben), sondern ausschließlich Zahlen vorliegen.

Im nächsten Beispiel werden zwei Potenzen mit gleichem Exponenten addiert. Dazu wird jede Potenz einzeln ausgerechnet und im Anschluss werden die beiden Potenzwerte addiert.

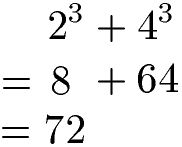
Hinweis: Die Addition von Potenzen mit ungleicher Basis und ungleichem Exponenten kann auch nur durchgeführt werden, wenn ausschließlich Zahlen vorliegen um die Potenzen auszurechnen.

Potenzen mit negativen Zahlen

Für die Addition von Potenzen mit negativen Exponenten werden die Koeffizienten addiert. Am Rest der Potenz ändert sich hingegen nichts.

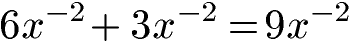
Alternativ kann eine Potenz mit negativem Exponenten in einen Bruch umgewandelt werden. Das Vorzeichen des Exponenten wird von negativ (-) auf positiv (+) vertauscht. Die x^-2 im Zähler werden zu x² im Nenner. Im Anschluss werden die Zähler addiert.

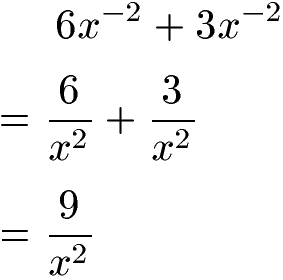
Sollten die Koeffizienten negativ sein kann ganz einfach addiert oder subtrahiert werden. Ein Beispiel:

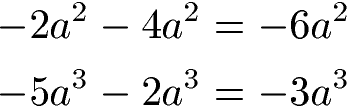
Weitere Inhalte:

• Potenzen subtrahieren
• Zur Mathematik-Übersicht