Quersumme / Quersummenregel

Mit der Quersumme befassen wir uns in diesem Artikel. Dabei liefere ich sowohl einige Beispiele als auch Quersummenregeln für die Teilbarkeit von Zahlen. Dieser Artikel gehört zu unserem Bereich Mathematik.

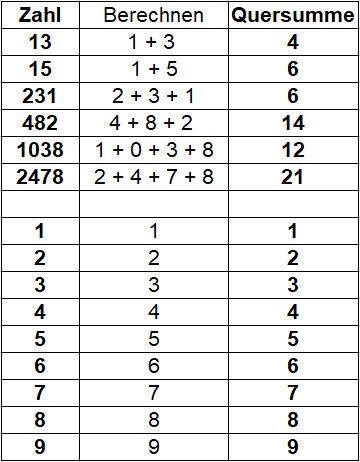
Die Quersumme ist die Summe der einzelnen Ziffern einer Zahl. Die nächste Tabelle zeigt die Quersumme von Zahlen wie 13 und 15, aber auch die Quersummen größerer Zahlen wie zum Beispiel 231 oder 1038. Die Quersumme einstelliger Zahlen ist immer die Zahl selbst.

Soweit zur Quersumme. Stellt sich als nächstes die Frage, was man denn mit diesen Quersummen anfängt? Und genau deshalb befassen wir uns nun noch mit den Teilbarkeitsregeln.

Quersumme und Quersummenregel

Es gibt mehrere Teilbarkeitsregeln welche die Quersumme einsetzen. Eine umfangreiche Darstellung zu diesem Thema findet ihr im Artikel Teilbarkeitsregeln.

Teilbarkeitsregel 3:

Eine Zahl ist ohne Rest durch 3 teilbar, wenn die Quersumme durch 3 ohne Rest teilbar ist.

Hinweis: Die Quersumme ist die Summe aller Ziffern (z.B. ist die Quersumme von 2356: 2 + 3 + 5 + 6 = 16).

Beispiele:

• Die Zahl 150 ist durch 3 teilbar, denn 1 + 5 + 0 = 6 und 6 ist durch 3 ohne Rest teilbar.
• Die Zahl 231 ist durch 3 teilbar, denn 2 + 3 + 1 = 6 und 6 ist durch 3 ohne Rest teilbar.
• Die Zahl 778 ist nicht durch 3 teilbar, denn 7 + 7 + 8 = 22 und 22 ist nicht ohne Rest durch 3 teilbar.

Teilbarkeitsregel 9:

Eine Zahl ist ohne Rest durch 9 teilbar, wenn die Quersumme durch 9 ohne Rest teilbar ist.

Hinweis: Die Quersumme ist die Summe aller Ziffern (z.B. ist die Quersumme von 2356: 2 + 3 + 5 + 6 = 16).

Beispiele:

• Die Zahl 153 ist durch 9 ohne Rest teilbar, denn 1 + 5 + 3 = 9 und 9 : 9 = 1.
• Die Zahl 515 ist nicht durch 9 ohne Rest teilbar, denn 5 + 1 + 5 = 11 und nicht durch 9 ohne Rest teilbar.

Links:

• Zur Mathematik-Übersicht