Rechnen bis 100

Welche Möglichkeiten hat man im Zahlenraum bis 100 Aufgaben einfach zu rechnen? Ich zeige dir dies für alle Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. Beispiele mit Erklärungen dazu bekommst du ebenfalls.

Werden die Zahlen etwas größer (also zum Beispiel beim Rechnen bis 100 oder 1000) tun sich viel Schüler sehr schwer. Es gibt jedoch die Möglichkeit sich das Leben etwas einfacher zu machen. Daher wird ab der 2. Klasse das halbschriftliche Rechnen verwendet um Rechenaufgaben einfacher ausrechnen zu können.

Rechnen bis 100 Addition:

Starten wir mit der Addition im Zahlenraum bis 100. Hier geht man so vor, dass man erst die Zehner addiert und danach die Einer.

Beispiel 1: Halbschriftliche Addition

Berechnet werden soll 12 + 26. Wir zerlegen die Aufgabe, indem wir erst die Zehner addieren. 10 + 20 = 30. Danach addieren wir noch die Einer mit 2 + 6 = 8. Beides rechnen wir zusammen: 30 + 8 = 38. Daher ist 12 + 26 = 38.

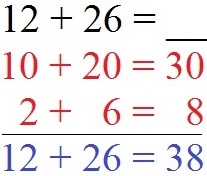
Im nächsten Abschnitt sehen wir und die Subtraktion bis 100 an.

Rechnen bis 100: Subtraktion

Sehen wir uns als nächstes die Subtraktion im Zahlenraum bis 100 an. Auch bei der Subtraktion wird eine Zerlegung der Aufgabe durchgeführt. Erst werden die Zehner abgezogen, danach die Einer.

Beispiel 2: Halbschriftliche Subtraktion

Berechnet werden soll 55 - 39. Die 39 zerlegen wir in 30 und 9. Von der 55 ziehen wir zunächst die 30 ab. Wir erhalten 55 - 30 = 25. Von den 25 ziehen wir im Anschluss noch die 9 ab. Wir rechnen 25 - 9 = 16. Daher ergibt 55 - 39 = 16.

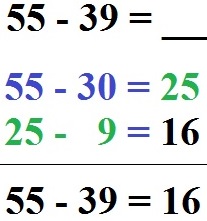
Als nächstes sehen wir uns die Multiplikation im Zahlenraum bis 100 an.

Bis 100 multiplizieren

Die halbschriftliche Multiplikation hilft dabei Multiplikationen im Zahlenraum bis 100 oder sogar noch etwas darüber hinaus durchführen zu können. Dies hilft vor allem auch da Schüler Zahlen die über 10 hinaus gehen oft nur schlecht multiplizieren können.

Beispiel 3: Multiplikation bis 100

Berechnet werden soll 3 · 12. Die 12 zerlegen wir in 10 und 2. Sowohl die 10 als auch die 2 multiplizieren wir mit der 3. Als Ergebnisse erhalten wir 30 und 6. Diese addieren wir zu 30 + 6 = 36. Daher ist 3 · 12 = 36.

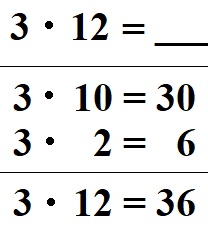
Fehlt uns noch die Division, welche wir in uns im nächsten Abschnitt sehen.

Dividieren bis 100

Sehen wir uns als nächstes die Division im Zahlenraum bis 100 an. Auch bei der Division wird eine Zerlegung der Aufgabe in Teilaufgaben durchgeführt.

Beispiel 4: Halbschriftliche Division

Berechnet werden soll 72 : 6. Die 72 zerlegen wir dabei in kleinere Zahlen, welche man einfach durch 6 teilen kann. Dazu gibt es natürlich verschiedene Möglichkeiten. Eine ganz einfache Möglichkeit besteht darin die 72 in 60 und 12 zu zerlegen. Sowohl die 60 als auch die 12 lassen sich einfach durch 6 teilen. Die Ergebnisse 10 und 2 addieren wir zu 12. Daher ist 72 : 6 = 12.

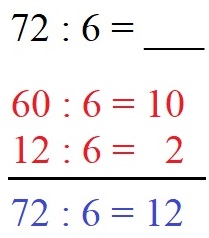
Weitere Beispiele - auch mit größeren Zahlen - findest du unter halbschriftlich Rechnen.

Aufgaben (Übungen) Rechnen bis 100

In diesem Abschnitt kannst du das Thema "Rechnen bis 100" noch ein bisschen üben. Du bekommst 4 Antwortmöglichkeiten auf eine Frage. Eine der Antworten ist richtig, die 3 anderen Antworten sind falsch.

Aufgabe 1:

• Wie lautet die Lösung dieser Aufgabe?
• 35 + 12 = ______

• 38
• 50
• 44
• 47

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.