Scheitelpunkt berechnen / ablesen: Formel und Parabel

In diesem Artikel befassen wir uns damit, wie man den Scheitelpunkt einer Parabel berechnen oder im einfachsten Falle ablesen kann. Entsprechende Formeln und Informationen werden anhand von Beispielen erläutert. Natürlich erfahrt ihr auch, was man unter dem Scheitelpunkt versteht. Dieser Artikel gehört zu unserem Bereich Mathematik.

Zunächst sollten wir uns einmal ansehen, was man unter dem Scheitelpunkt eigentlich versteht. Dazu nehmen wir uns eine Parabel, die einmal nach oben und nach unten geöffnet ist. Der höchste Punkte und der tiefste Punkt sind dabei markiert. Dies sind die Scheitelpunkte.

Hier liegt der Scheitelpunkt unten und ist mit S markiert:

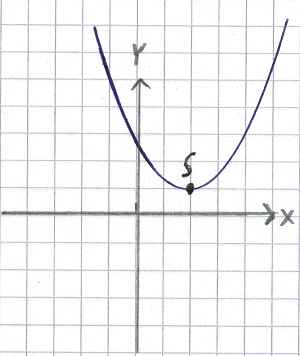
Hier liegt der Scheitelpunkt oben und ist ebenfalls mit S markiert:

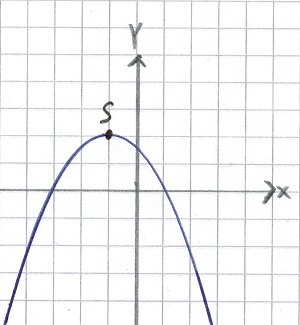
Jedem sollte nun klar sein, was der Scheitelpunkt ist. Wir können uns also nun damit befassen, wie man den Scheitelpunkt findet. Wer mit den folgenden Inhalten Probleme hat, der sollte einmal die folgende Liste an Themen durchsehen. Wer diese noch nicht beherrscht kann gerne nachlesen: quadratische Funktionen, PQ-Formel und Mitternachtsformel.

Scheitelpunkt ablesen (aus Gleichung)

Man kann in manchen Fällen den Scheitelpunkt aus einer Gleichung ablesen. Dazu muss sich die Gleichung in einer bestimmten Form befinden oder man muss die Gleichung ganz einfach auf diese Form bringen. Genau diese Form bezeichnet man als Scheitelform oder Scheitelpunktform. Sie lautet:

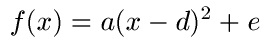
Dann liegt der Scheitelpunkt bei:

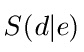
Beispiel 1:

Gegeben sei die Gleichung f(x) = 1(x - 2)² + 4. Lies den Scheitelpunkt S ab.

Lösung:

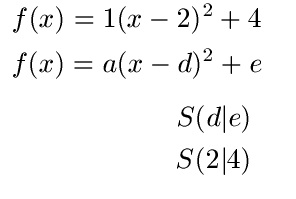
Der Scheitelpunkt liegt hier also bei x = 2 und y = 4. Dies war durch simples ablesen möglich.

Beispiel 2:

Gegeben sei die Funktion f(x) = 2(x + 3)² - 5. Wo liegt hier der Scheitelpunkt S?

Lösung:

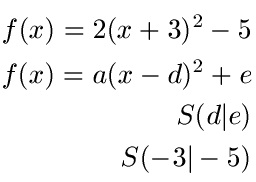
Der Scheitelpunkt liegt hier also bei x = -3 und y = -5. Dies kommt daher, dass in der Gleichung des Beispiels die Rechenzeichen/Vorzeichen umkehrt sind als in der allgemeinen Scheitelpunktform.

Hinweis: In einem weiteren Artikel befassen wir uns damit, wie man Gleichungen auf die Scheitelpunktform bringt.

Scheitelpunkt berechnen: Form für PQ-Formel

Kann man den Scheitelpunkt auch berechnen? Klar. Dafür nehme wir eine quadratische Funktion bzw. eine quadratische Gleichung, die in der Form für die PQ-Formel oder die ABC-Formel vorliegt. Auch hier sehen wir uns die Berechnung und Beispiele an.

Scheitelpunkt berechnen:

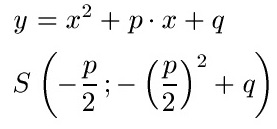
Beispiel 3:

Sehen wir uns auch hierzu ein Beispiel an. Wo liegt der Scheitelpunkt bei der Gleichung y = x² - 2x + 3?

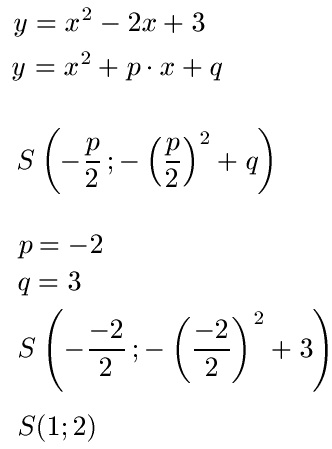
Um den Scheitelpunkt zu bestimmen lesen wir p und q ab. Dabei ist p = -2 und q = 3. Dies setzen wir ein und erhalten den Scheitelpunkt bei x = 1 und y = 2.

Scheitelpunkt berechnen: Form für Mitternachtsformel

Eine weitere Möglichkeit soll jetzt vorgestellt werden. Dabei liegt die Gleichung in der Form vor, auf die man die ABC-Formel bzw. Mitternachtsformel anwenden kann.

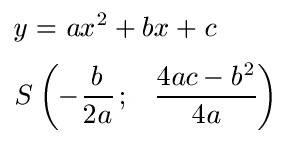
Beispiel 4:

Wo liegt der Scheitelpunkt bei der Aufgabe f(x) = -x² - 2x - 1?

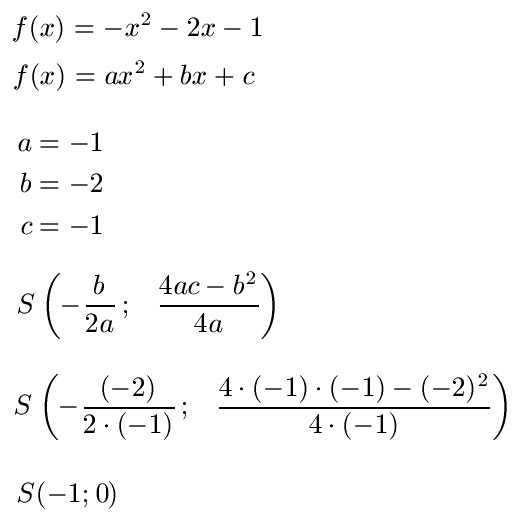
Wir ermitteln a = -1, b = -2 und c= -1. Dies setzen wir ein um den Scheitelpunkt zu bestimmen.

Scheitelpunkt berechnen mit Ableitung

Es gibt noch eine weitere Möglichkeit den Scheitelpunkt zu bestimmen. Wie wir am Anfang des Artikels gesehen haben, ist der Scheitelpunkt an der Stelle des Hochpunktes oder Tiefpunktes der Funktion bzw. Gleichung. Daher kann man den Scheitelpunkt auch mit Hilfe der Differentialrechnung bestimmen. Wie dies - zum Beispiel bei einer Normalparabel - gemacht wird seht ihr im Artikel Hochpunkt + Tiefpunkt.

Links:

• Zur Mathematik-Übersicht