Extremwerte: Hochpunkt + Tiefpunkt

Extremwerte, so genannte Hochpunkte und Tiefpunkte werden bei der Auswertung von Funktionen eingesetzt. Warum man dies überhaupt macht und wie es funktioniert, lernt ihr in diesem Artikel der Mathematik.

Im nun folgenden gehen wir auf die Begriffe Extremwert, Hochpunkt und Tiefpunkt ein. Damit ihr diesen Artikel jedoch verstehen könnt, solltet ihr einige Vorkenntnisse mitbringen. Wem die folgenden Artikel noch gar nichts sagen, der möge sie bitte nachlesen. Alle anderen können gleich mit den Extremwerten starten.

• Funktionen zeichnen
• Grundlagen: Was hat es mit der Steigung auf sich?
• Faktorregel und Summenregel
• Produktregel und Quotientenregel
• Kettenregel
• Tabelle von Ableitungen
• Erste und zweite Ableitung

Extremwerte Video:
Dieser Artikel liegt auch als Video vor.

• Hinweise: Dies ist noch ein Tafelvideo. Eine Neuauflage in HD ist geplant. Der Abruf ist auch direkt in der Rubrik Extremwerte Video möglich.
• Probleme: Bei Abspielproblemen bitte den Artikel Video Probleme aufrufen.

Was ist ein Extremwert?

Im Mathematik-Unterricht musstet Ihr mit Sicherheit schon die eine oder andere Funktion zeichnen. Dazu wurde in der Regel eine Wertetabelle angelegt und die Funktion anschließend in ein Koordinatensystem eingezeichnet. Oftmals erwischt man beim zeichnen jedoch nicht den höchsten oder tiefsten Punkt einer Funktion. Durch Kenntnisse in der Extremwert-Rechnung kann man dieses Problem lösen, in dem man diese Extrempunkte berechnet. Das Wissen aus diesem Bereich wird in vielen Branchen eingesetzt. Hier ein paar Anwendungen:

• Lässt sich der Umsatzverlauf eines Produktes durch eine Funktion beschreiben, kann man deren Minimum bzw. Maximum bestimmen.
• Es lassen sich Materialeinsparungen erzielen, in dem man mit möglichst wenig Blech eine möglichst große Dose baut.
• Die Funktion einer Spannung an einem technischen System ist bekannt. Durch Extremwert-Rechnung lässt sich der Zeitpunkt der Maximallast finden.

Minima und Maxima

In der Extremwert-Rechnung unterscheidet man zwischen lokalen und globalen Maximas bzw. Minimas. Um dies besser zu verstehen, werft einen Blick auf die folgende Grafik:

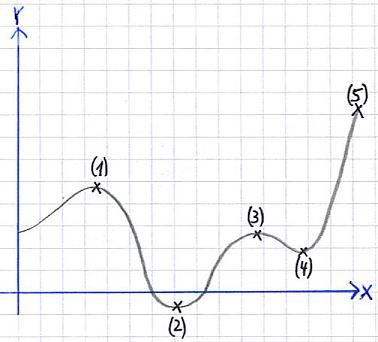
Die wichtigen Punkte wurden mit den Zahlen 1 bis 5 versehen. Diese schauen wir uns nun einzeln an:

• Bei (1) befindet sich ein Maximum. Genauer gesagt ist es ein lokales Maximum, denn es handelt sich hier nicht um den höchsten Punkt der dargestellten Funktion, sondern nur um den höchsten Punkt in der näheren Umgebung.
• Bei (2) findet sich ein lokales Minimum, denn dieser Punkt ist der tiefste Punkt in diesem Bereich. Da (2) jedoch auch den tiefsten Punkt der kompletten Funktion darstellt, ist (2) nicht nur ein lokales Minimum, sondern sogar ein globales Minimum.
• Bei (3) findet sich erneut ein lokales Maximum.
• Bei (4) findet sich ein lokales Minimum.
• Bei (5) findet Ihr das globale Maximum, denn es handelt sich um den höchsten Punkt der gezeichneten Funktion.

In diesem Zusammenhang spricht man oft vom Monotonieverhalten einer Funktion. Sieht man sich die Funktion genauer an, hat man immer dann einen Hochpunkt, wenn erst eine Steigung ( monoton wachsend ) des Funktionsgraphen vorliegt und anschließend ein Abfall ( monoton fallend ). Umgekehrt erhält man einen Tiefpunkt, wenn die Steigung erst monoton fallend ist und anschließend monoton wachsend. An den lokalen Minima und Maxima ist die Steigung stets Null. Diese Eigenschaft macht man sich bei der Extremwert-Berechnung zu nutze.

Hochpunkt und Tiefpunkt

Eben haben wir gesehen: An den lokalen Minima und Maxima ist die Steigung Null. Dies ist eine wichtige Erkenntnis, sie reicht allerdings nicht aus. So wie die Funktion an den lokalen Extremwertstellen ihr Monotonieverhalten ( siehe letzter Absatz ) ändert, wechselt die 1. Ableitung an den lokalen Extremstellen Ihr Vorzeichen. Dabei ist die Ableitungsfunktion f' an einer lokalen Minimumstelle monoton wachsend. Aus diesem Grund muss f''(x₀) > 0 sein. Bei einer lokalen Maximumstelle ist die erste Ableitung hingegen monoton fallend. Aus diesem Grund ist in diesem Fall f''(x₀) < 0.

Anhand zweier Beispiele soll nun die Berechnung von Hochpunkten und Tiefpunkten gezeigt werden. Dabei liegt immer eine Funktion der Form y = f(x) vor. Die Vorgehensweise sieht wie folgt aus:

1. Wir bilden die erste Ableitung der Funktion
2. Wir bilden die zweite Ableitung der Funktion
3. Wir setzen die erste Ableitung Null, sprich f'(x) = 0. Dadurch erhalten wir einen oder mehrere X-Werte.
4. Diese X-Werte setzen wir in die zweite Ableitung ein und prüfen damit, ob wir einen Hochpunkt oder Tiefpunkt haben.

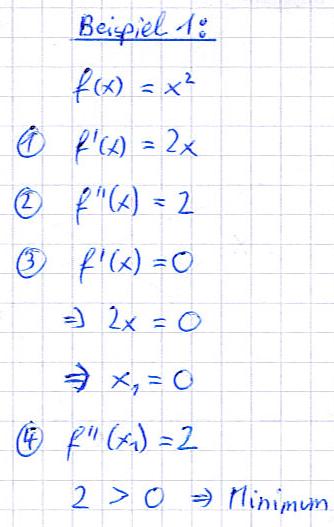
Anmerkung: Setzt man den gefundenen X-Wert noch in die Startgleichung f(x) = x² ein, kann man damit y = x² = 0² = 0 bestimmen. Das Minimum liegt somit bei P = ( 0; 0 )

Gleich weiter zum zweiten Beispiel:

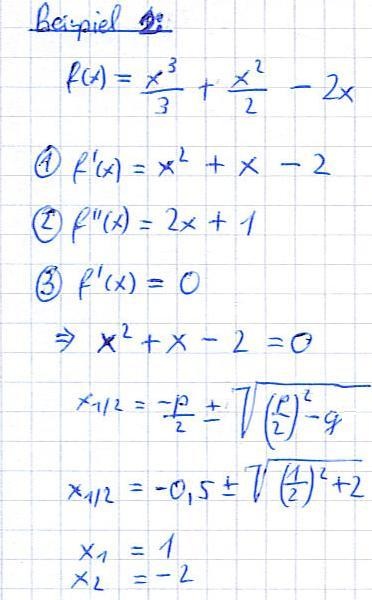
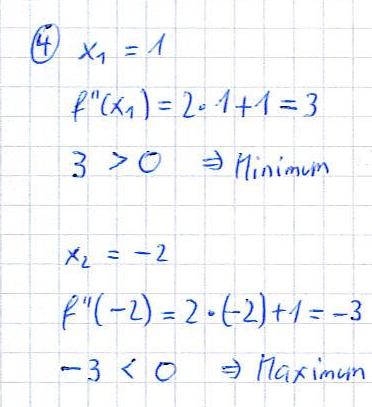
Auch hier kann man x₁ = 1 und x₂ = -2 in f(x) einsetzen. Damit ergibt sich der Minimum-Punkt P₁ = ( 1 ; -1,167 ) und der Maximum Punkt P₂ = ( -2; 3.33 ).

Links:

• Zur Ableitung-Übersicht
• Zur Mathematik-Übersicht