Sehnenviereck mit Beispiel

In diesem Artikel geht es um das Sehnenviereck. Wir beschäftigen uns mit den Eigenschaften eines Sehnenvierecks und wie man Formeln zu dessen Berechnung einsetzt. Dieser Artikel gehört zu unserem Bereich Mathematik Mittelstufe.

In den folgenden Abschnitten befassen wir uns mit dem Sehnenviereck. Zuvor solltet ihr jedoch wissen, was ein Viereck überhaupt ist. Aus diesem Grund empfehle ich zunächst den folgenden Artikel zu lesen:

• Rechnen am Viereck

Sehnenviereck Eigenschaften

Bei einem Sehnenviereck liegen alle Eckpunkte auf dem Umkreis. Außerdem ist die Summe der Gegenwinkel 180°. Es gilt auch die Umkehrung dieser Aussage: Alle Eckpunkte liegen auf einem Kreis, wenn die Summe je zweier Gegenwinkel 180 Grad beträgt. Auf Basis der folgenden Grafik gilt damit:

• α + γ = 180°
• β + δ = 180°
• α + γ + β + δ = 360°

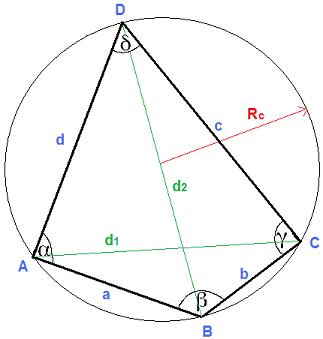
Für das Sehnenviereck gelten eine ganze Reihe an Formeln. Dies werden im nun Folgenden angegeben und beziehen sich auf die dargestellte Grafik. Wichtig: Alle Längenangaben sollten in der selben Einheit eingesetzt werden, sonst kommt bei der Berechnung ein falsches Ergebnis raus.

Umfang Formel:

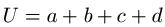
Beispiel: Der Umfang eines Sehnenvierecks soll berechnet werden. Dabei sind die Längen der Seiten a = 3cm, b = 2cm, c = 6cm und d = 8cm. Damit berechnet sich der Umfang zu:

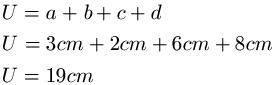
Radius des Umkreises / Umkreisradius Formel:

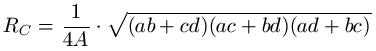
In der Formel stellt "R_C" den Radius des Umkreises dar, "A" ist die Fläche und die Angaben a, b, c und d sind die Längen der Seiten, wie in der Grafik dargestellt.

Diagonalen Formel:

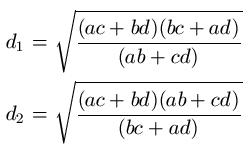
In der Formel sind d₁ und d₂ die Längen der Diagonalen. Darüber hinaus gibt es noch die Seitenlängen a, b, c und d des Vierecks.

Fläche Formel:

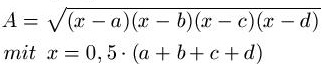
Unter "A" versteht man die Fläche, d₁ und d₂ sind die Längen der Diagonalen. Für a, b, c und d werden die Längen des Vierecks abgelesen. Um die Formel nicht völlig unübersichtlich werden zu lassen, wird in die Formel zur Berechnung der Fläche auch ein "x" eingesetzt. Dieses x sollte zuerst berechnet werden und anschließend die Fläche berechnen.

Satz des Ptolemäus:

Das Produkt der Diagonalen ist gleich der Summe aus den Produkten der Gegenseiten. Es gilt:

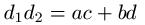
Links:

• Zur Geometrie Übersicht
• Zur Mathematik-Übersicht