Standardabweichung berechnen

Wie kann man die Standardabweichung berechnen? Genau dies sehen wir uns in den nächsten Abschnitten genauer an. Ein Beispiel bzw. eine Aufgabe wird dabei ausführlich vorgerechnet und erklärt. Natürlich erfahrt ihr auch noch, wofür man die Standardabweichung überhaupt braucht. Dieser Artikel gehört zu unserem Bereich Mathematik.

Die Standardabweichung ist ein Begriff aus der Statistik bzw. Wahrscheinlichkeitsrechnung oder Stochastik. Mit ihr kann man ermitteln, wie stark die Streuung der Werte um einen Mittelwert ist. Ein entsprechendes Beispiel wird dies gleich verdeutlichen. Zunächst sollte man jedoch noch folgendes Wissen. Um die Standardabweichung zu berechnen, müssen wir vorher erst den Durchschnitt berechnen (arithmetisches Mittel sagen Mathematiker dazu) und im Anschluss noch die Varianz.

Standardabweichung berechnen:

• 1. Schritt: Den Durchschnitt berechnen.
• 2. Schritt: Die Varianz berechnen.
• 3. Schritt: Die Standardabweichung berechnen.

In dieser Reihenfolge muss man vorgehen. Machen wir das an einem Beispiel.

Standardabweichung Beispiel bzw. Aufgabe

Marc schreibt eine Woche lang auf, wie lange er von zuhause in die Schule gebraucht hat: Am Montag waren es 8 Minuten, am Dienstag 7 Minuten, am Mittwoch 9 Minuten, Donnerstag 10 Minuten und Freitag 6 Minuten. Wie hoch ist die Standardabweichung? Was sagt das Ergebnis aus?

Lösung: Um die Aufgabe zu lösen, wenden wir den 3-Schritt-Plan von weiter oben an.

Schritt 1: Zunächst müssen wir den Durchschnitt berechnen. Dazu addieren wir zunächst alle Zeitangaben von Montag bis Freitag. Außerdem teilen wir dies durch die Anzahl der Tage. Da dies fünf Werte sind, teilen wir also durch 5. Dies sieht dann so aus:

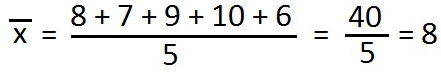
Im Durchschnitt benötigt Marc also 8 Minuten um zur Schule zu gelangen.

Schritt 2: Mit dem Durchschnitt können wir nun die Varianz berechnen. Hinweis: Die Varianz gibt die mittlere quadratische Abweichung der Ergebnisse um ihren Mittelwert an. Um dies zu tun, nehmen wir wieder unsere fünf Werte vom Anfang (also 8, 7, 9, 10 und 6) und ziehen von diesen jeweils den Durchschnitt (8) ab. Dies müssen wir dann jeweils quadrieren (hoch 2) und die Summe bilden. Am Ende teilen wir noch durch die Anzahl der Werte, die wir ursprünglich genommen hatten, sprich wir teilen wieder durch 5.

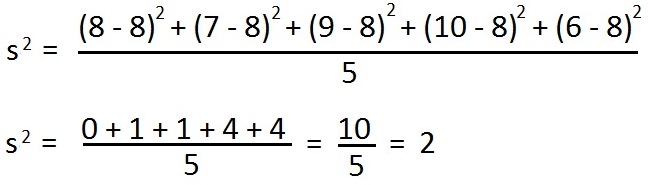
Die Varianz - also die mittlere quadratische Abweichung - beträgt damit 2.

Schritt 3: Die Standardabweichung fehlt noch. Dazu ziehen wir aus der Varianz die (quadratische) Wurzel. Natürlich interessiert nur das positive Ergebnis.

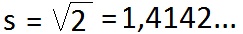
Interpretation: Die Standardabweichung vom Durchschnitt - das waren 8 Minuten - beträgt etwa 1,4 Minuten. Für den Schulweg benötigt Marc also stets ähnlich lang, die Schwankung ist relativ gering.

Neben der Standardabweichung gibt es noch weitere interessante Werte, wie zum Beispiel den Erwartungswert. Diesen und viele weitere Themen findet ihr in unserer Stochastik Übersicht bzw. Statistik Übersicht.

Weitere Links:

• Zur Mathematik-Übersicht