Strahlensätze: Lösungen der Aufgaben

Hier findet Ihr nun die Lösungen der Aufgaben und Übungen zu den Strahlensätzen der Mathematik. Dabei benötigt Ihr sowohl die Formeln des 1.Strahlensatzes, wie auch des 2.Strahlensatzes. Bei Problemen solltet Ihr auf alle Fälle noch einmal in unseren Erklärungsartikel rein sehen und die Lösungen erst zur Not einsehen.

• Zu den Erklärungen "Strahlensätze"
• Zurück zur Aufgabenstellung

Lösung Aufgabe 1: Beantworte die Fragen

1a) Wie lauten die Formeln für den 1. Strahlensatz?

• |SA₁| : |SA₂| = |SB₁| : |SB₂|
• |SA₁| : |A₁A₂| = |SB₁| : |B₁B₂|
• |SA₂| : |A₁A₂| = |SB₂| : |B₁B₂|

1b) Wie lauten die Formeln für den 2. Strahlensatz?

• |A₁B₁| : |A₂B₂| = |SA₁| : |SA₂|
• |A₁B₁| : |A₂B₂| = |SB₁| : |SB₂|

Lösung Aufgabe 2: Berechne die Aufgaben

2a) Die Entfernung von "S" zu "A₁" beträgt 3,40cm. Die Entfernung von "S" zu "A₂" beträgt 6,00cm. Und von "S" zu "B₁" haben wir 3,8cm Entfernung. Wie lang ist die Strecke |SB₂|?

• Aus dem Text entnehmen wir: |SA₁| = 3,40cm
• Aus dem Text entnehmen wir: |SA₂| = 6,00cm
• Aus dem Text entnehmen wir: |SB₁| = 3,80cm
• Einsetzen: |3,40cm| : |6,00cm| = |3,80cm| : |SB₂|
• 1. Schritt: 0,567 = 3,80 : SB₂
• 2. Schritt: 0,567 · SB₂ = 3,80
• 3. Schritt: SB₂ = 3,80 : 0,567
• 4. Schritt: SB₂ = 6,7cm

2b) Turm-Aufgabe: Bekannt sind die Längen a, b und t. Zu dem herrscht zwischen a und t ein rechter Winkel, der auch auf der Grafik eingetragen wurde. Ziel ist es nun, mit den Strahlensätzen die Höhe des Turms zu berechnen. Dabei sei a = 2 m, b = 3 m und t = 20 m. Wie hoch ist der Turm?

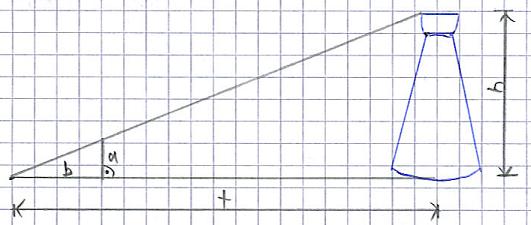
• Die Strecke "a" entspricht "A₁B₁"
• Die Strecke "h" entspricht "A₂B₂"
• Die Strecke "b" entspricht "SA₁"
• Die Strecke "t" entspricht "SA₂"
• Einsetzen in: |A₁B₁| : |A₂B₂| = |SA₁| : |SA₂|
• Liefert: 2m : h = 3m : 20m
• Liefert nach h umgestellt: h =13,33m

Links:

• Zurück zur Mathematik-Übersicht