Strahlensätze zur Streckenberechnung

Die Strahlensätze dienen dazu, Längen von Strecken zu bestimmen. Was es genau damit auf sich hat und was sich hinter dem 1.Strahlensatz und dem 2.Strahlensatz verbirgt, erklären wir euch in diesem Artikel Anhand von Grafiken, Text und Beispielen.

Wie bereits in der Einleitung des Artikels angedeutet, dienen die beiden Strahlensätze dazu, die Entfernung von Strecken zu bestimmen. Dabei bedient man sich Wissen aus der Geometrie. Die Herleitung zum Strahlensatz beschränken wir hier auf ein Minimum. In der Schule wird in erster Linie verlangt, den 1. Strahlensatz und den 2. Strahlensatz anzuwenden. Heißt: Es werden Entfernungen und Längen vorgegeben und eine weitere Strecke muss mit diesen ausgerechnet werden. Das Schwierige beim Strahlensatz ist meist nicht das Einsetzen von Zahlen in die Gleichungen, sondern überhaupt zu erkennen, dass man den Strahlensatz anwenden darf. Für alle, die noch Probleme mit dem Umstellen von Gleichungen haben oder nicht Wissen, was sich hinter den Grundlagen der Geometrie verbirgt, raten wir die folgenden Artikel zu lesen. Alle anderen können sich dies sparen:

• Geometrie
• Gleichungen lösen

1. Strahlensatz

In der Mathematik unterscheidet man zwei Strahlensätze. Mit dem 1.Strahlensatz möchten wir hier beginnen. Schaut euch dazu erst einmal die folgende Grafik genau an. Wie diese zu Stande kommt, wird unterhalb des Bildes erklärt:

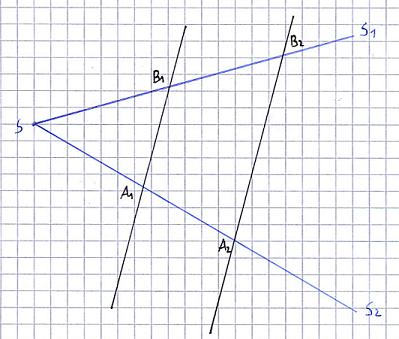
Wie das Bild vom 1. Strahlensatz entstand:

• Es wurde ein Punkt "S" auf dem Blatt eingezeichnet
• Von diesem Punkt "S" wurden zwei Strahlen gezeichnet, die nicht parallel sind
• Diese beiden Strahlen wurden mit "S1" und "S2" bezeichnet
• Eine vertikale Gerade wird eingezeichnet, die beide Strahlen in den Punkten "A1" und "B1" schneidet
• Zu dieser vertikalen Gerade wie eine weitere, parallele Gerade gezogen, welche die Strahlen in "A2" und "B2" schneidet

Wie dieses Bild entsteht, habt ihr soeben erfahren. Nun wird es Zeit, dieses auch zu benutzen. Im nun folgenden findet ihr Verhältnisformeln. Das zwischen den "| ... |" stehende ist eine Längenangabe. Beispiel: |SA₁| bedeutet, dass ihr hier der Abstand vom Punkt "S" zum Punkt "A₁" einsetzen müsst. Es folgen alle Formeln des 1. Strahlensatzes.

1. Strahlensatz Formeln:

• |SA₁| : |SA₂| = |SB₁| : |SB₂|
• |SA₁| : |A₁A₂| = |SB₁| : |B₁B₂|
• |SA₂| : |A₁A₂| = |SB₂| : |B₁B₂|

Beispiel:

Die Entfernung von "S" zu "A₁" beträgt 3,40cm. Die Entfernung von "S" zu "A₂" beträgt 6,00cm.  Und von "S" zu "B₁" haben wir 3,8cm Entfernung. Wie lang ist die Strecke |SB₂|?

Lösung:

• Aus dem Text entnehmen wir: |SA₁| = 3,40cm
• Aus dem Text entnehmen wir: |SA₂| = 6,00cm
• Aus dem Text entnehmen wir: |SB₁| = 3,80cm
• Einsetzen:  |3,40cm| : |6,00cm| = |3,80cm| : |SB₂|
• 1. Schritt:  0,567  = 3,80 : SB₂
• 2. Schritt:  0,567 · SB₂ = 3,80
• 3. Schritt: SB₂ = 3,80 : 0,567
• 4. Schritt: SB₂ = 6,7cm

Aus dem Text wurden somit erst die Längeninformationen entnommen. Danach wurden diese in die oberste Gleichung des 1.Strahlensatzes eingesetzt. Und nun ging es nur darum, nach der Unbekannten in der Gleichung umzustellen.

2. Strahlensatz

Der erste Strahlensatz liefert leider keine Informationen dazu, wie das Längenverhältnis A₁B₁ zu A₂B₂ ist. Deshalb wurde von den Mathematikern noch der 2. Strahlensatz definiert. Auch hier zunächst eine kleine Grafik, die im Anschluss erklärt wird:

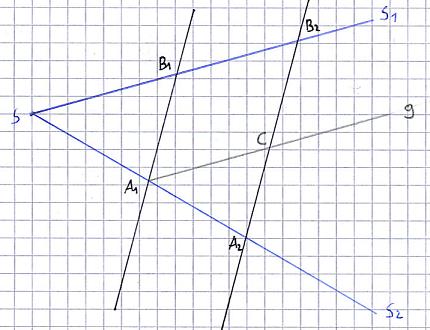
Wie das Bild vom 2. Strahlensatz entstand:

• Es wurde ein Punkt "S" auf dem Blatt eingezeichnet
• Von diesem Punkt "S" wurden zwei Strahlen gezeichnet, die nicht parallel sind
• Diese beiden Strahlen wurden mit "S1" und "S2" bezeichnet
• Eine vertikale Gerade wird eingezeichnet, die beide Strahlen in den Punkten "A1" und "B1" schneidet
• Zu dieser vertikalen Gerade wie eine weitere parallele Gerade gezogen, welche die Strahlen in "A2" und "B2" schneidet
• Eine Parallele "g" wird parallel zu S1 gezogen und zwar so, dass Sie durch den Punkt A1 geht
• Der Schnittpunkt zur Strecke |B₂A₂| wurde mit "C" bezeichnet

Durch diesen "Trick" lassen sich noch die Formeln des 2. Strahlensatzes angegeben:

2. Strahlensatz Formeln:

• |A₁B₁| : |A₂B₂| = |SA₁| : |SA₂|
• |A₁B₁| : |A₂B₂| = |SB₁| : |SB₂|

Anwendung des Strahlensatzes

Zu guter Letzt noch ein ( von Mathelehrern gerne genutztes ) Beispiel zur Nutzung des Strahlensatzes. Bei diesem soll die Höhe eines Turms berechnet werden. Hier erst einmal eine Grafik:

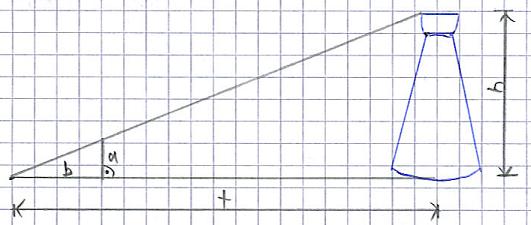
Bekannt sind die Längen a, b und t. Zu dem herrscht zwischen a und t ein rechter Winkel, der auch auf der Grafik eingetragen wurde.  Ziel ist es nun, mit den Strahlensätzen die Höhe des Turms zu berechnen. Dabei sei a = 2m, b = 3m, t = 20, h = ?

Lösung: Schaut auf die Strahlensatz Grafik und vergleicht

• Die Strecke "a" entspricht "A₁B₁"
• Die Strecke "h" entspricht "A₂B₂"
• Die Strecke "b" entspricht "SA₁"
• Die Strecke "t" entspricht "SA₂"
• Einsetzen in: |A₁B₁| : |A₂B₂| = |SA₁| : |SA₂|
• Liefert: 2m : h = 3m : 20m
• Liefert nach h umgestellt: h =13,33m

Tipp: Den meisten Schülern und Schülerinnen fällt die Anwendung des Strahlensatzes zunächst recht schwer. Deshalb meine Empfehlung: Rechnet unsere Übungen und Aufgaben zum Thema um Sicherheit zu bekommen.

Links:

• Zu den Übungsaufgaben "Strahlensatz"
• Zurück zur Mathematik-Übersicht