Symmetrie zur Y-Achse

Mit der Symmetrie zur Y-Achse befassen wir uns diesem Artikel. Dabei wird erklärt, was man unter der Symmetrie zur Y-Achse versteht und es werden Beispiele vorgestellt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Die Funktionskurve einer geraden Funktion ist spiegelsymmetrisch zur Y-Achse angeordnet. Dies bedeutet, dass jeder auf der Kurve gelegene Punkt durch Spiegelung an der Y-Achse wieder in einen Kurvenpunkt übergeht. Mathematisch findet man solch eine Funktion wenn gilt: f(-x) = f(x). Aber was bedeutet dies nun? Beginnen wir mit einer einfachen Grafik mit y = x² bei der an der roten Linie - also an der Y-Achse - die Spiegelung durchgeführt wird. Spiegelt man den Punkt auf der rechten Seite, so liegt der gespiegelte Punkt auf der anderen Seite ebenfalls auf der Kurve.

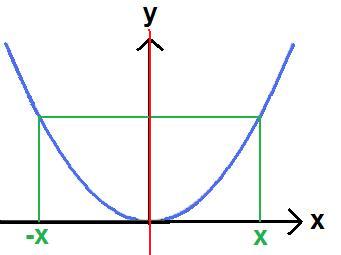
So eine Grafik mag ja schön und nett sein. Aber es ist doch viel zu umständlich jede Funktion zu zeichnen und sich das Anzusehen? Richtig. Also berechnen wir ob eine Funktion zur Y-Achse eine Symmetrie aufweist oder eben nicht. Hinweis: Gilt f(x) = f(-x) so wird die Funktion auch als gerade bezeichnet.

Symmetrie zur Y-Achse rechnerisch

Eine Symmetrie zur Y-Achse finden wir heraus, in dem wir f(x) = f(-x) setzen und nachsehen, ob auf beiden Seiten der Gleichung dann der selbe Ausdruck steht. Zum besseren Verständnis rechne ich einmal ein paar Beispiele vor.

Beispiel 1:

Ist die Funktion f(x) = x² zur Y-Achse symmetrisch oder nicht? Dazu ermitteln wir zunächst f(-x) und im Anschluss setzen wir f(x) = f(-x).

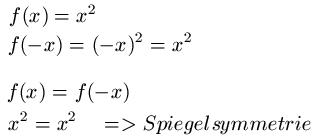
Beispiel 2:

Ist die Funktion f(x) = x² + 3 zur Y-Achse symmetrisch oder nicht? Dazu ermitteln wir wieder f(-x) und im Anschluss setzen wir f(x) = f(-x).

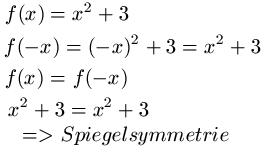
Beispiel 3:

Ist die Funktion f(x) = x + 2 zur Y-Achse symmetrisch oder nicht? Dazu ermitteln wir wieder f(-x) und im Anschluss setzen wir f(x) = f(-x).

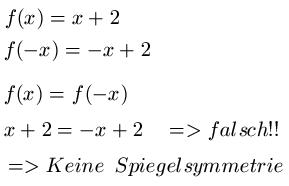
Ich hoffe die Beispiele haben dabei geholfen den Zusammenhang zu verstehen.

Links:

• Zur Ableitung-Übersicht
• Zur Mathematik-Übersicht