Symmetrie zum Ursprung

Mit der Symmetrie zum Ursprung befassen wir uns diesem Artikel. Dabei wird erklärt, was man unter der Symmetrie zum Ursprung versteht und es werden Beispiele vorgestellt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Beginnen wir erst einmal mit einer kurzen Definition bevor wir uns eine Grafik und Beispiele ansehen. Eine Funktion y = f(x) mit einem symmetrischen Definitionsbereich D heißt ungerade, wenn für jedes x ε D die Bedingung f(-x) = -f(x) erfüllt ist. In diesem Fall ist die Funktion auch punktsymmetrisch zum Koordinatenursprung. Die folgende Grafik zeigt die Funktion y = x³. Wir nehmen uns nun einen Punkt auf deren Verlauf und spiegeln diesen am Koordinatenursprung ( roter Punkt ). Tun wir dies, erhalten wir einen weiteren Punkt, der ebenfalls auf dem Kurvenverlauf liegt. Wir haben also eine Symmetrie zum Ursprung. Seht euch also nun einmal die Grafik an:

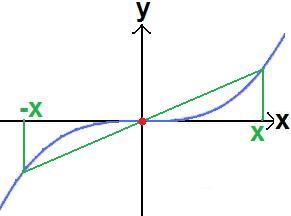
Soweit zur Grafik. Aber es ist doch sicherlich viel zu kompliziert eine Funktion immer zu zeichnen und dann nachzusehen, ob eine Symmetrie zum Ursprung vorliegt? Richtig. Genau aus diesem Grund geht es im nächsten Abschnitt darum rechnerisch herausfinden, ob eine Symmetrie zum Ursprung vorliegt.

Symmetrie zum Ursprung berechnen

Wie kann man nun berechnen, ob eine Symmetrie zum Ursprung vorliegt oder nicht? Dazu setzen wir f(-x) = -f(x) und sehen ob die Gleichung wahr ist. Damit hätten wir eine ungerade Funktion, welche punktsymmetrisch zum Koordinatenursprung ist. Die folgenden Beispiele werden dies hoffentlich verdeutlichen.

Beispiel 1:

Die Funktion f(x) = x³ soll auf eine Symmetrie zum Ursprung hin untersucht werden. Dazu ermitteln wir zunächst f(-x) und -f(x).  Danach setzen wir f(-x) = -f(x). Ist die Gleichung korrekt, dann liegt eine Punktsymmetrie ( also eine Symmetrie zum Ursprung ) vor.

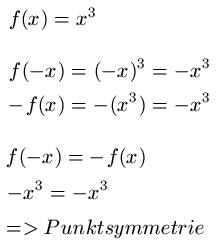
Beispiel 2:

Die Funktion f(x) = -3x³ +2x soll auf eine Punktsymmetrie zum Ursprung untersucht werden. Dazu ermitteln wir zunächst f(-x) und -f(x).  Danach setzen wir f(-x) = -f(x). Ist die Gleichung korrekt, dann liegt eine Symmetrie zum Ursprung vor.

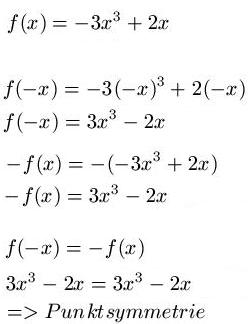
Beispiel 3:

Die Funktion f(x) = x² + x soll auf eine Symmetrie zum Ursprung hin untersucht werden. Dazu ermitteln wir zunächst f(-x) und -f(x).  Danach setzen wir f(-x) = -f(x). Ist die Gleichung korrekt, dann liegt eine Symmetrie zum Ursprung vor.

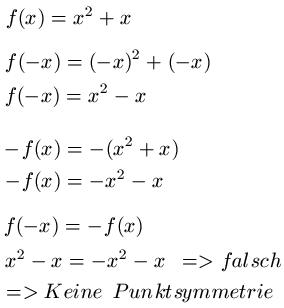
Ich hoffe die Beispiele haben dabei geholfen den Zusammenhang zu verstehen.

Links:

• Zur Ableitung-Übersicht
• Zur Mathematik-Übersicht