Umkehrfunktion Ableitung

Mit dem Ableiten einer Umkehrfunktion befassen wir uns in diesem Artikel. Dabei zeige ich durch Einsatz von Beispielen wie dies funktioniert. Dieser Artikel gehört zu unserem Bereich Mathematik.

Bevor wir hier an die Ableitung der Umkehrfunktion gehen solltet ihr überhaupt erst einmal wissen, was eine Umkehrfunktion ist. Und natürlich wäre es sehr hilfreich einige gängige Ableitungsregeln zu beherrschen. Sofern ihr Probleme mit dem folgenden Artikel zur Ableitung der Umkehrfunktion habt empfehle ich zunächst die folgenden Links zu lesen. Wer die Umkehrfunktion schon kennt und grundlegend ableiten kann, der braucht das natürlich nicht.

• Umkehrfunktion
• Faktorregel + Summenregel

Ableitung der Umkehrfunktion

Anhand von zwei wirklich typischen Beispielen möchte ich euch gleich die Ableitung der Umkehrfunktion zeigen. Zunächst jedoch die allgemeine Gleichung und einen Plan zur Vorgehensweise.

Gleichung Ableitung Umkehrfunktion:

Liegt eine umkehrbare Funktion der Form y = f(x) vor und ist zugleich x = g(y) die nach x umgeformte Darstellung dieser Funktion dann gilt:

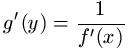
Der Nenner - also f'(x) - darf hier natürlich nicht Null werden. Darüber hinaus muss - wie bereits weiter oben geschrieben - die Funktion überhaupt umkehrbar sein.

Allgemeine Vorgehensweise:

1. Wir schreiben uns y = f(x) auf
2. Wir leiten f(x) ab und erhalten y' = f'(x)
3. Wir stellen f(x) nach x um
4. Wir setzen in die Gleichung f'(x) ein
5. Wir ersetzen den Ausdruck von f'(x) durch y
6. Wir vertauschen x und y

Umkehrfunktion ableiten Beispiele

Die eben gezeigte Gleichung sowie die allgemeine Vorgehensweise soll nun auf Beispiele angewendet werden. Zur besseren Übersicht schreibe ich vor jede Berechnung noch den jeweiligen Schritt aus der "allgemeinen Vorgehensweise". Ich empfehle neben dem PC auf einem Stück Papier noch einmal die Aufgabe selbst mitzurechnen.

Beispiel 1:

Gegeben sei die Funktion y = f(x) = e^x. Gesucht ist nun die Ableitung der Umkehrfunktion. Wir schreiben für den ersten Schritt die Aufgabe ab und leiten die Funktion für den zweiten Schritt ab. Da die Ableitung von e^x wieder e^x ist sollten hier keine Verständnisprobleme auftreten. Im dritten Schritt lösen wie y = e^x nach x auf. Dazu benötigen wir den natürlichen Logarithmus, den wir auf beide Seite anwenden. Wir erhalten dadurch x = ln(y).

Beim vierten Schritt setzen wir in die oben genannte Gleichung für f'(x) nun e^x ein, so wie wir dies im zweiten Schritt berechnet haben. Wir erhalten dadurch g'(y) = 1 durch e^x. Aus der Aufgabenstellung wissen wir, dass y = e^x ist. Somit können wir in Schritt 5 für e^x nun einfach y einsetzen. Im letzten Schritt tauschen wir einfach noch y durch x aus und erhalten dadurch die Ableitung der Umkehrfunktion. Das sieht dann also so aus:

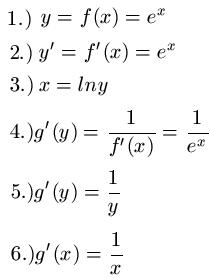
Beispiel 2:

Gegeben sei die Funktion y = f(x) = tan x . Gesucht ist nun die Ableitung der Umkehrfunktion. Aus der Formelsammlung entnehmen wir die Ableitung zu f'(x) = tan²x + 1. Für den dritten Punkt stellen wir y = tan x nach x um und erhalten x = arctan(y). Mit den gewonnen Informationen gehen wir bei Punkt 4 in die oben genannte Formel.  Für den Punkt 5.) muss man wissen, dass wir am Anfang y = tan x da stehen hatten und wir damit aus tan²x nun y² machen können. Im letzten Schritt tauschen wir y durch x aus.

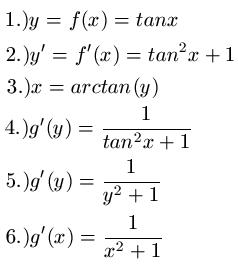
Links:

• Zur Mathematik-Übersicht