Urnenmodell

Mit dem Urnenmodell befassen wir uns in diesem Artikel. Dabei erklären wir euch, was man unter dem Urnenmodell versteht und liefern euch passende Rechenbeispiele. Dieser Artikel gehört zum Bereich Mathematik / Stochastik.

Unter einem Urnenmodell versteht man einen "Kasten", in dem sich Kugeln befinden. Aus dem Kasten werden nun - ohne das man reinsieht - Kugeln gezogen und deren Nummer notiert. Man unterscheidet grundsätzlich zwei verschiedene Versuche:

1. Urnenmodell mit zurücklegen: Aus der Urne wird eine Kugel gezogen. Die Nummer wird aufgeschrieben und im Anschluss wird die Kugel wieder in die Urne geworfen. Die Anzahl der Kugel in der Urne bleibt somit gleich.
2. Urnenmodell ohne zurücklegen: Aus der Urne wird eine Kugel gezogen. Die Nummer wird aufgeschrieben und im Anschluss wird die Kugel weggeworfen. Bei jeder Ziehung reduziert sich somit die Anzahl der Kugeln in der Urne.

Hinweis: Die Idee des Urnenmodells kann man auch auf andere Probleme übertragen. Zum besseren Verständnis belassen wir es in diesem Artikel jedoch bei dem Ziehen von Kugeln aus einer Urne.

Urnenmodell mit zurücklegen

Für das Urnenmodell mit zurücklegen gilt: Aus der Urne wird eine Kugel gezogen. Die Nummer wird aufgeschrieben und im Anschluss wird die Kugel wieder in die Urne geworfen. Die Anzahl der Kugeln in der Urne bleibt somit gleich. Folgende Regel gilt für diesen Fall: Wird aus einer Urne mit n Kugeln die Anzahl k Kugeln entnommen, so ergeben sich g = n^k Möglichkeiten für eine geordnete Stichprobe.

Beispiel 1: Möglichkeiten

In einer Urne befinden sich 26 Kugeln. Es soll insgesamt 4 mal gezogen werden, wobei die Kugel stets wieder in dir Urne zurückgelegt wird. Wie viele Möglichkeiten der Entnahme gibt es ?

Lösung: Wir haben 26 Kugeln und ziehen 4 mal. Damit ergibt sich g = 26 · 26 · 26 · 26 = 26⁴ = 456976 Möglichkeiten.

Jetzt kann es natürlich passieren, dass wir nicht alle Kugeln aus der Urne ziehen. Nach dem ziehen legen wir diese jedoch wieder zurück. Auch für diesen Fall gibt es eine Formel zur Berechnung der Möglichkeiten. Bei dieser benötigen wir den so genannten Binomialkoeffizienten. Wer diesen noch nicht kennt, findet gleich noch die passende Rechenvorschrift. Die Überlegung ist die Folgende: Aus einer Urne mit n Kugeln entnehmen wir eine ungeordnete Stichprobe vom Umfang k. Dadurch berechnet sich die Anzahl der Möglichkeiten zu:

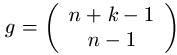
Beispiel 2: Stichprobe

Wir haben eine Urne mit 8 Kugeln und ziehen 5 mal in einer ungeordneten Stichprobe. Wie viele Möglichkeiten gibt es?

Lösung: Dem Text entnehmen wir, dass n = 8 und k = 5 ist. Diese Werte setzen wir in die Formel ein und berechnen die Lösung.

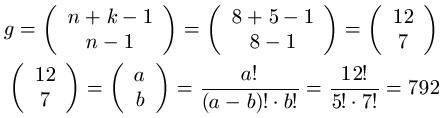
Urnenmodell ohne zurücklegen

Für das Urnenmodell ohne zurücklegen gilt: Aus der Urne wird eine Kugel gezogen. Die Nummer wird aufgeschrieben und im Anschluss wird die Kugel weggeworfen. Bei jeder Ziehung reduziert sich somit die Anzahl der Kugeln in der Urne. Folgende Regel gilt für diesen Fall: Wird aus einer Urne mit n Kugeln der Umfang  n entnommen - sprich es werden alle Kugeln gezogen - so ergeben sich g = n! Möglichkeiten für eine geordnete Stichprobe. Hinweis: Für alle, die mit dem "!" nichts anfangen können, steht der Artikel Fakultät bereit.

Beispiel 1: Möglichkeiten

Wir haben eine Urne mit 5  Kugeln. Alle 5  Kugeln werden ohne zurücklegen gezogen, es wird eine geordnete Stichprobe entnommen. Wie viele Möglichkeiten gibt es für die Ziehung?

Lösung: Wir berechnen die Möglichkeiten zu g = 5! = 5 · 4 · 3 · 2 · 1 = 120 Möglichkeiten

Jetzt kann es natürlich passieren, dass wir nicht alle Kugeln aus der Urne ziehen. Auch für diesen Fall gibt es eine Formel zur Berechnung der Möglichkeiten. Bei dieser benötigen wir den so genannten Binomialkoeffizienten. Wer diesen noch nicht kennt, findet gleich noch die passende Rechenvorschrift. Die Überlegung ist die Folgende: Wird aus einer Urne mit n Kugel eine ungeordnete Stichprobe vom Umfang k entnommen, so ergibt sich die folgende Anzahl an Möglichkeiten:

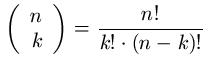
Beispiel 2: Stichprobe

Wir haben eine Urne mit 10 Kugeln und ziehen 6 Kugeln aus dieser ohne zurück zulegen. Wie viele Möglichkeiten gibt es?

Lösung: Wir entnehmen der Aufgabenstellung, dass n = 10 und k = 6 ist und setzen dies in die Formel ein.

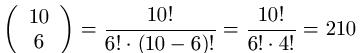
Links:

• Zur Stochastik-Übersicht
• Zurück zur Mathematik-Übersicht