Wertemenge / Wertebereich bestimmen

In diesem Artikel geht es um die Wertemenge bzw. den Wertebereich. Dabei wird erklärt was man darunter versteht und es werden Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

Mir Erläuterungen zu Wertemenge und Wertebereich befassen wir uns in den nächsten Abschnitten. Um dies verstehen zu können solltet ihr wissen, wie man eine Funktion zeichnet und was es mit linearen und quadratischen Funktionen auf sich hat. Wem dies noch nicht klar ist, kann dies in den folgenden Artikeln nachlesen.

• Funktion zeichnen
• Lineare Funktionen
• Quadratische Funktionen

Erklärung als Video:
Dieses Thema liegt auch als Video vor. In diesem werden typische Aufgabenstellungen und Beispiele vorgestellt. Per Button kann auch in den Vollbildmodus gewechselt werden. Das Video ist auch direkt in der Sektion Wertemenge/Wertebereich Video aufrufbar. Bei Abspielproblemen hilft der Artikel Video Probleme.

Was sind Wertemenge / Wertebereich?

Erst einmal eine kurze Vorwarnung: Die Definition von Wertemenge bzw. Wertebereich ist leider nicht ganz eindeutig. In der Mathematik der Schule interessiert man sich meistens für alle Y-Werte, die eine Funktion annehmen kann. Das ist aber nicht immer so. Im Zweifelsfall bitte den Lehrer bzw. die Lehrerin noch einmal danach fragen. Stellt sich nun die Frage: Wie bekomme ich denn alle Y-Werte raus? Dazu sehen wir uns einige Beispiele an und ermitteln diese Werte auf grafischem wie auch rechnerischem Wege.

Beispiel 1:

Als erstes werfen wir einen Blick auf die Funktion f(x) = y = x². Also eine Parabel. Diese zeichnen wir in ein Koordinatensystem ein. Und dabei sehen wir, dass die Y-Werte nur Null oder größer sind.

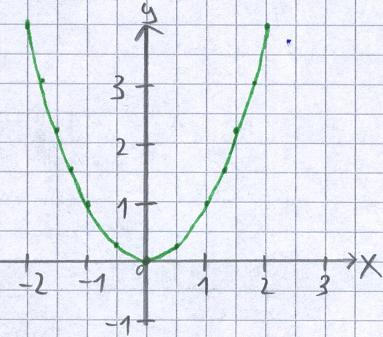
Wie man hier sehen kann, liegt bei x = 0 und y = 0 der tiefste Wert für y vor. Manchmal kann man dies jedoch nicht so einfach sehen. Ist dies der Fall, muss man mit Hilfe von Ableitungen den Hochpunkt und Tiefpunkt zur Funktion finden. Auch hilft es das Verhalten der Funktion am Definitionsbereich bzw. gegen plus und minus Unendlich zu untersuchen. Aus der Grafik und der Funktion sieht man, dass die Y-Werte von Null bis Unendlich laufen können. Damit gilt für den Wertebereich: W = [ 0, ∞ )

Beispiel 2:

Nun sehen wir uns y = -x² an. Auch hier haben wir eine Parabel, die jedoch nach unten hin geöffnet ist. Die y-Werte können dabei y = 0 nicht nach oben hin überschreiten. Damit ist y = 0 der größte Wert für y. Nach unten hin können die Werte hingegen bis ins Unendliche laufen, also bis minus unendlich. Damit gilt für den Wertebereich: W = ( -∞, 0 ]

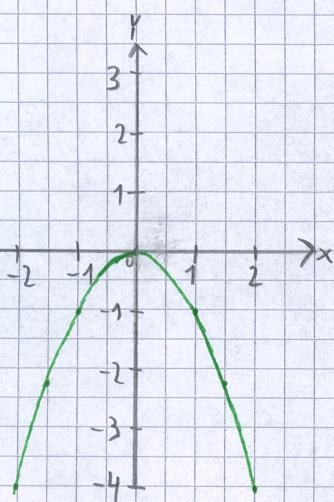
Beispiel 3:

Es wird Zeit für ein etwas anspruchsvolleres Beispiel: f(x) = y = 3x · e^{-2x +1}. Auch hier soll die Wertemenge bzw. der Wertebereich bestimmt werden. Die folgende Grafik zeigt den interessanten Bereich der Funktion. Dabei sieht man, dass die Funktion von "unten" her kommt, irgendwo zwischen 1,0 und 2,0 ihr Maximum haben muss und danach wieder abfällt. Geht man mit einer Wertetabelle an die Sache dran, so wird es sehr schwierig wirklich den höchsten Punkt zu treffen. Daher gehen wir die Sache gleich rechnerisch an. Zunächst aber erst einmal die Grafik:

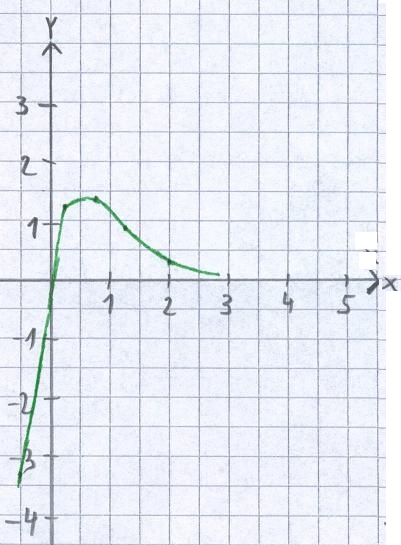
Um wirklich den höchsten Punkt zu finden, suchen wir nach Hochpunkten und Tiefpunkten. Dazu leiten wir die Funktion zweimal ab, setzen die erste Ableitung Null und finden x₁ = 0,5. Damit gehen wir in die zweite Ableitung und finden heraus, dass wir wirklich einen Hochpunkt haben. Mit den Informationen gehen wir in f(x) und finden bei y = 1,5 den Hochpunkt und höchsten Punkt. Damit gilt für den Wertebereich: W = ( -∞, 1,5 ]

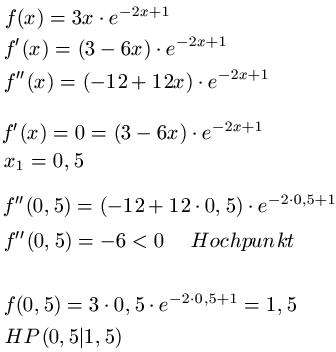
Links:

• Wertebereich / Wertemenge Aufgaben + Übungen
• Zur Mathematik-Übersicht