Winkeltypen / Winkelarten

Mit verschiedenen Winkeltypen bzw. Winkelarten befassen wir uns in diesem Artikel. Dabei sollen vor allem Beispiele zum besseren Verständnis dienen. Dieser Artikel gehört zu unserem Bereich Mathematik Mittelstufe.

Mit verschiedenen Arten von Winkeln befassen wir uns in diesem Artikel. Wir erklären euch also, welche Winkeltypen es gibt. Zuvor solltet ihr jedoch wissen, was überhaupt ein Winkel ist. Aus diesem Grund empfehle ich zunächst den folgenden Artikel zu lesen:

• Winkel und Geodreieck

Winkelarten und Winkeltypen im Überblick

Beginnen wie mit verschiedenen Winkeltypen bzw. Winkelarten. Es folgt dabei zunächst ein kleiner Überblick und im Anschluss werden diese verschiedenen Winkeltypen auch noch einmal grafisch gezeigt:

• Nullwinkel: α = 0°
• Spitzer Winkel:  0° < α < 90°
• Rechter Winkel: α = 90°
• Stumpfer Winkel: 90° < α < 180°
• Gestreckter Winkel: α = 180°
• Überstumpfer Winkel: 180° < α < 360°
• Vollwinkel: α = 360°

Die folgenden Grafiken zeigen nun die verschiedenen Winkelarten:

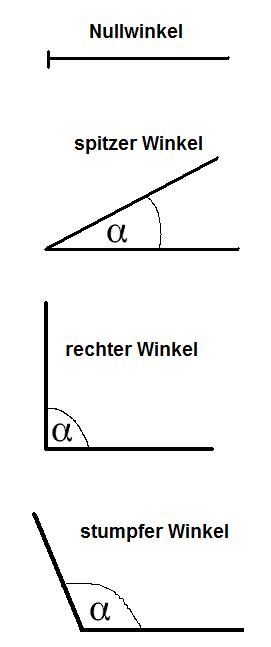
Wir haben eben den Nullwinkel, den spitzen Winkel, den rechten Winkel, den stumpfen Winkel, den gestreckten Winkel, den überstumpfen Winkel und den Vollwinkel kennen gelernt. Neben diesen sieben Winkelarten gibt es noch weitere Beschreibungen zu Winkeltypen, bei denen es jedoch darum geht, wie sich verschiedene Winkel zueinander verhalten. Dazu mehr im nun folgenden Abschnitt.

Scheitelwinkel, Nebenwinkel, Stufenwinkel und Wechselwinkel

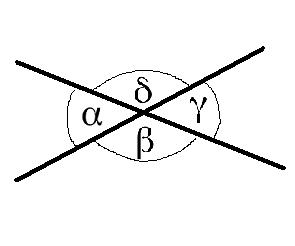
Der Scheitelwinkel: Schneiden sich zwei Geraden, so bezeichnet man das Paar gegenüberliegender Winkel als Scheitelwinkel oder Gegenwinkel. Scheitelwinkel sind immer gleich groß. In der folgenden Grafik sind die Winkel α und γ sowie β und δ Scheitelwinkel.

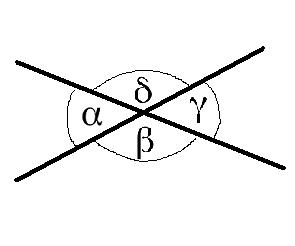
Der Nebenwinkel: In der Grafik kann man zu dem auch Nebenwinkel erkennen. Dabei bezeichnet man zwei nebeneinander liegende Winkel als Nebenwinkel. Die Summe zweier Nebenwinkel beträgt 180º. In der folgenden Grafik sind zum Beispiel α und β oder auch δ und γ Nebenwinkel. Ergänzen sich zwei Winkel zu 180°, so bezeichnet man dies als Supplementwinkel. Ergibt die Summe hingegen nur 90°, so heißen sie Komplementwinkel.

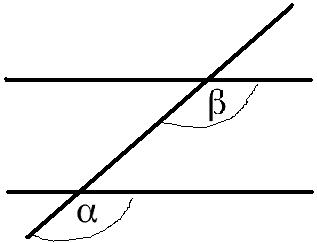
Der Stufenwinkel: Wir haben nun zwei parallele Geraden, die durch eine Gerade geschnitten wird. Dabei bildet sich ein Stufenwinkel aus. In der folgenden Grafik werden diese als α und β bezeichnet.

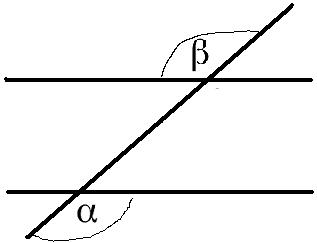
Der Wechselwinkel: Wir haben nun zwei parallele Geraden, die durch eine Gerade geschnitten wird. Dabei bildet sich ein Wechselwinkel aus. In der folgenden Grafik werden diese als α und β bezeichnet.

Links:

• Winkelarten / Winkeltypen Aufgaben
• Zur Mathematik-Übersicht