Aufleiten Regeln ( Aufleitung )

Mit den verschiedenen Regeln zum Aufleiten beschäftigen wir uns in diesem Artikel. Dabei befassen wir uns mit diesen Regeln in Kurzform und im Anschluss an jedes Gebiet findet ihr Links um euch - bei Bedarf - noch ausführlicher zu informieren. Dieser Artikel gehört zum Bereich Mathematik Oberstufe.

Tipp: Dieser Artikel stellt wichtige Integrationsregeln kurz vor. Ausführliche Informationen, Beispiele und Videos dazu findet ihr in dem jeweiligen Artikel, der unter der jeweiligen Regel verlinkt ist.

Zunächst ein wichtiger Hinweis: Der Begriff "Aufleiten" ist umgangssprachlich. Er wird von vielen Schülern einfach als das Gegenteil von Ableiten angesehen. In der Mathematik spricht man bei diesem Bereich richtigerweise von Integration bzw. von Integrationsregeln. Dieser Artikel hier richtet sich also mehr an Schüler bzw. Studenten, die sich der Sache von der Umgangssprache her genähert haben.

Es gibt in der Mathematik eine Reihe an Regeln zum Aufleiten. In diesem Artikel sollen genau diese Aufleitungsregeln einmal in Kurzform vorgestellt werden. Unterhalb der jeweiligen Regel findet ihr dann einen Link zu weiteren Informationen.

Regel zum Aufleiten: Potenzregel

Beginnen wir bei mit der Aufleitungsregel für Potenzen. Dabei wird hier zunächst eine Konstante integriert:

• f(x) = 2 -> F(x) = 2x + C
• f(x) = 5 -> F(x) = 5x + C
• f(x) = 8 -> F(x) = 8x + C

Merke: Eine Konstante wird aufgeleitet, in dem man an die Konstante ein "x" angehängt und +C schreibt. Das C steht dabei für eine beliebige Zahl. Lasst dieses C erst einmal so stehen, wie es ist. Der Grund: Leitet ihr nun 2x + 2 oder 2x + 5 bzw. allgemein 2x + C ab, erhaltet ihr wieder f(x) = 2.

Nun möchten wir Funktionen wie zum Beispiel f(x) = 2x  oder f(x) = 3x² integrieren. Dafür benutzen wir die Potenzregel, die wie folgt aussieht:

Beispiele:

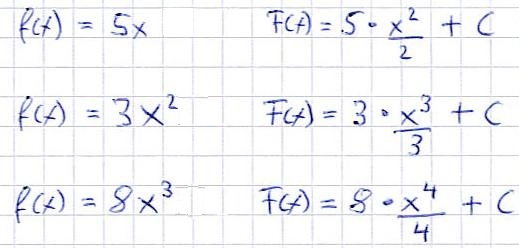
• Weitere Informationen: Potenzregel Artikel anzeigen

Summenregel zum Aufleiten

Wie auch bei der Summenregel der Differentation gibt es bei der Aufleitung auch eine Summenregel, die sehr ähnlich aussieht. Diese besagt, dass ihr Gliedweise aufleiten dürft. Wie immer sind einige Beispiele für das Verständnis vermutlich am Besten:

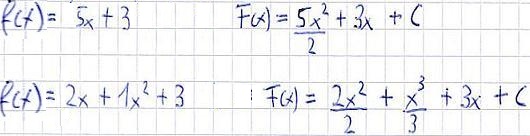
• Weitere Informationen: Summenregel Artikel anzeigen

Aufleitung durch Partielle Integration

Soll ein Produkt aufgeleitet werden, wendet man die so genannte Partielle Integration - oft auch Produktintegration - an. Ich hoffe ihr erinnert euch an die Produktableitung ( Differentation ). So etwas ähnliches gibt es auch bei der Integration - also beim Aufleiten - und wird als partielle Integration bezeichnet. Es folgt zunächst die allgemeine Formel, im Anschluss gibt es einige Beispiele.

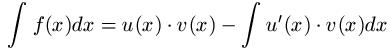
Zeit für ein paar Beispiele um die partielle Integration zu zeigen. Dazu gleich eine kleine Warnung:  Ihr müsst am Anfang u und v' festlegen. Wählt ihr diese falsch herum aus, könnt ihr die Aufgabe unter Umständen nicht mehr lösen. Tauscht in diesem Fall u und v' einmal gegeneinander aus und versucht es erneut.

Beispiel 1:

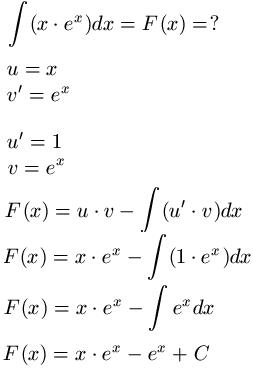
• Weitere Informationen: Artikel zur partiellen Integration

Links:

• Flächenberechnung durch Integration
• Zur Integrations-Übersicht
• Zur Mathematik-Übersicht