Binomische Formeln Faktorisieren / Ausklammern

Mit dem Faktorisieren bzw. Ausklammern bei Binomischen Formeln befassen wir uns in diesem Artikel. Dabei wird auf einfache Art und Weise und anhand von Beispielen gezeigt, wie man die Binomischen Formeln sozusagen "rückwärts" anwenden kann. Dieser Artikel gehört zu unserem Bereich Mathematik.

In diesem Artikel geht es nun darum, dass ihr zum Beispiel auf einen Ausdruck wie 4x² + 12x + 9 die Binomischen Formeln rückwärts anwendet. Dabei entsteht ein Ausdruck mit Klammern. Ich zeige gleich Beispiele für alle 3 Binomischen Formeln und wie man dies auf einfache Art und Weise umsetzt. Eines sollte jedoch gleich klar sein: Nicht immer kann man einen solchen Ausdruck so umformen, dass man eine der drei bekannten Binomischen Formeln auch anwenden kann. Eine kleine Warnung: Ich stelle hier einen einfachen und praktischen Weg vor um die Aufgaben zu lösen, 100% "schöne" Mathematik wird hier daher nicht gezeigt.

Erklärung als Video:
Dieses Thema liegt auch als Video vor. In diesem werden typische Aufgabenstellungen und Beispiele vorgestellt. Per Button kann auch in den Vollbildmodus gewechselt werden. Das Video ist auch direkt in der Sektion Binomische Formeln: Ausklammern/Faktorisieren Video aufrufbar. Bei Abspielproblemen hilft der Artikel Video Probleme.

1. Binomische Formel Faktorisieren

Eine kurze Erinnerung zur ersten Binomischen Formel. Hier lautet der mathematische Zusammenhang ( a + b )² = a² + 2ab + b². Und genau diese Gleichung werden wir nun anwenden, um eine Faktorisierung bzw. ein Ausklammern durchzuführen. Zum besseren Verständnis gleich anhand von Beispielen.

Beispiel 1:

Im ersten Beispiel soll 4x² + 12x + 9 auf die Form ( a + b )² gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a² = 4x² und b² = 9 und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 12x und setzen für a und b noch entsprechend ein. Da die Kontrolle stimmt, ist das Ergebnis richtig und wir können die Lösung notieren. Das sieht also dann so aus:

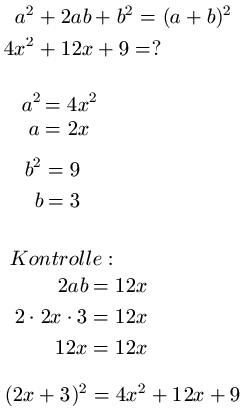
Beispiel 2:

Im zweiten Beispiel soll 9x² + 12xy + 4y² auf die Form ( a + b )² gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a² = 9x² und b² = 4y² und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 12xy und setzen für a und b noch ein. Da die Kontrolle stimmt, ist das Ergebnis richtig und wir können die Lösung notieren. Das sieht also dann so aus:

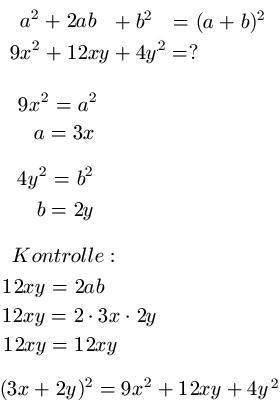
Beispiel 3:

Im dritten Beispiel soll 9x² + 14xy + 4y² auf die Form ( a + b )² gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a² = 9x² und b² = 4y² und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 14xy und setzen für a und b noch ein. Da die Kontrolle nicht stimmt, ist das Ergebnis falsch!! Die erste Binomische Formel kann hier also nicht eingesetzt werden. Das sieht also dann so aus:

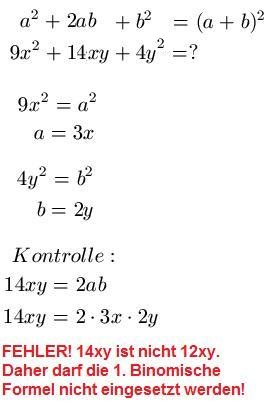
2. Binomische Formel Faktorisieren

Kommen wir als nächstes zur Faktorisierung der 2. Binomischen Formel. Für diese lautete der mathematische Zusammenhang: ( a - b )² = a² - 2ab + b². Und genau auf diese Form bringen wir nun wieder einige Beispiele.

Beispiel 4:

Im vierten Beispiel soll 16x² - 72xy + 81y² auf die Form ( a - b )² gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a² = 16x² und b² = 81y² und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 72xy und setzen für a und b noch ein. Da die Kontrolle stimmt, ist das Ergebnis richtig und wir können die Lösung notieren. Das sieht also dann so aus:

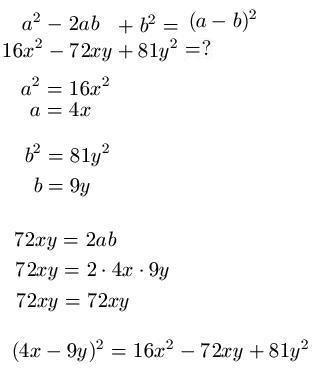
Beispiel 5:

Im fünften Beispiel soll 16x² - 80xy + 81y² auf die Form ( a - b )² gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a² = 16x² und b² = 81y² und berechnen jeweils das positive Ergebnis für a und b. Zur Kontrolle setzen wir noch 2ab = 80xy und setzen für a und b noch ein. Da die Kontrolle nicht stimmt, ist das Ergebnis falsch und wir können die Lösung verwerfen. Das sieht also dann so aus:

3. Binomische Formel Ausklammern

Fehlt uns noch das Ausklammern bzw. Faktorisieren bei der 3. Binomischen Formel. Die Vorgehensweise sieht ähnlich aus zu den schon vorgestellten Beispielen. Für die letzte Formel gilt der Zusammenhang: ( a + b ) ( a - b ) = a² - b². Auch hier sehen wir uns gleich einmal Beispiele an.

Beispiel 6:

Im sechsten Beispiel soll 9x² - 4y² auf die Form ( a + b )( a - b ) gebracht werden. Dazu schreiben wir uns den mathematischen Zusammenhang erst einmal hin, gefolgt von der Aufgabenstellung. Wir setzen a² = 9x² und b² = 4y² und berechnen jeweils das positive Ergebnis für a und b. Das sieht also dann so aus:

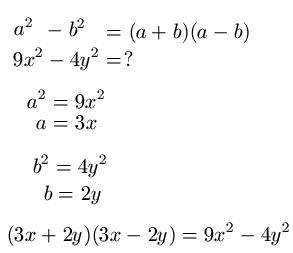
Links:

• Übungen: Binomische Formeln
• Zur Mathematik-Übersicht