Definitionslücke / Hebbare Definitionslücke, Pole etc.

In diesem Artikel geht es um Definitionslücken, hebbare Definitionslücken, Pole und Nullstellen. Dabei erkläre ich die Begriffe zunächst und zeige anhand von Beispielen wie man damit umgeht. Dieser Artikel gehört zu unserem Bereich Mathematik.

Im Artikel Pole und Nullstellen bin ich bereits grundlegend auf Pole und Nullstellen eingegangen. In diesem Artikel soll dies noch ausführlicher behandelt werden und außerdem gehe ich auf Definitionslücken bzw. hebbare Definitionslücken näher ein. Alles soll durch Beispiele verdeutlicht werden.

Erklärung als Video:
Dieses Thema liegt auch als Video vor. In diesem werden entsprechende Beispiele vorgestellt. Per Button kann auch in den Vollbildmodus gewechselt werden. Das Video ist auch direkt in der Sektion Hebbare Definitionslücke Video aufrufbar. Bei Abspielproblemen hilft der Artikel Video Probleme.

Begriffe und gebrochenrationale Funktionen

Wir sehen uns nun so genannte gebrochenrationale Funktionen an. Bei diesen interessieren wir uns für Nullstellen, Pole und ( hebbare ) Definitionslücken. Zunächst sollen die Begriffe erläutert werden.

• Nullstellen: Eine gebrochenrationale Funktion besitzt überall dort eine Nullstelle, wo das Zählerpolynom den Wert Null annimmt und das Nennerpolynom einen Wert ungleich Null annimmt.
• Pole: Polstellen einer gebrochenrationalen Funktion sind Stellen, an denen das Nennerpolynom verschwindet und gleichzeitig das Zählerpolynom einen von Null verschiedenen Wert annimmt.
• Definitionslücke: Hat die Nennerfunktion für einen bestimmten Wert eine Nullstelle und ist die Funktion an dieser Stelle damit nicht definiert, so bezeichnet man diese Stelle als Definitionslücke. Dies kann dann ein Pol sein ( Siehe Definition Pol ) oder eine hebbare Definitionslücke ( Siehe Definition hebbare Definitionslücke ).
• Hebbare Definitionslücke: Haben Zähler und Nenner gemeinsame Nullstellen so zerlegt man beide in Linearfaktoren und kürzt. Damit kann man Definitionslücken beheben und den Definitionsbereich erweitern.

Um nun eine gebrochenrationale Funktion auf Nullstellen, Pole und ( hebbare ) Definitionslücken zu untersuchen muss man also jeweils erst einmal die Nullstellen von Zähler und Nenner finden. Dazu nutzt man zum Beispiel Wege wie Ausklammern, PQ-Formel, Mitternachtsformel, Polynomdivision etc. Anhand einiger Beispiele soll dies nun gezeigt werden.

Beispiele: ( Hebbare ) Definitionslücken, Pole und Nullstellen

Zum besseren Verständnis einige Beispiele für ( hebbare ) Definitionslücken, Pole und Nullstellen.

Beispiel 1:

Gegeben sei die gebrochenrationale Funktion ( x + 1 ) : ( x² - x - 6 ). Zunächst setzen wir den Zähler gleich Null. Dabei erhalten wir x₁ = -1. Auch den Nenner setzen wir gleich Null. Mit der PQ-Formel erhalten wir x₂ = 3 und x₃ = -2. Da die Werte verschieden sind liegt für x₁ = -1 eine Nullstelle vor. Und x₂ = 3 und x₃ = -2 sind die Pole der Funktion.

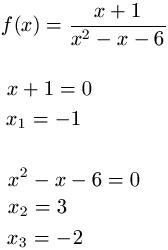
Beispiel 2:

Im zweiten Beispiel soll f(x) = ( x² + 4x + 3 ) : ( x³ + x² - 6x ) untersucht werden. Auf den Zähler können wir die PQ-Formel anwenden. Wir erhalten damit x₁ = -1 und x₂ = -3. Im Nenner können wir ein x ausklammern. Damit erhalten wir gleich x₃ = 0, denn setzen wir 0 ein wird der Nenner sofort Null. Außerdem berechnen wir x² + x - 6 = 0 mit der PQ-Formel und erhalten x₄ = 2 und x₅ = -3. Sehen wir uns nun die Ergebnisse an. Wir erhielten x₂ = x₅ = -3 und haben an dieser Stelle somit eine hebbare Lücke. Dann verbleiben wegen x₁ = -1 noch eine Nullstelle und mit x₃ = 0 und x₄ = 2 noch zwei Polstellen.

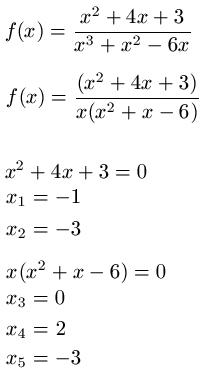
Beispiel 3:

Im nächsten Beispiel soll f(x) = ( 2( x - 2 )² ) : (( x - 1 )( x - 2)) untersucht werden. Da wir im Zähler ( x - 2 ) und im Nenner ( x - 2 ) haben liegt bei x = 2 ein hebbare Definitionslücke / Lücke vor. Kürzen wir ( x - 2 ) erhalten wir noch 2 ( x - 2 ) im Zähler und ( x - 1 ) im Nenner. Damit haben wir bei x = 2 noch eine Nullstelle und x = 1 eine Polstelle.

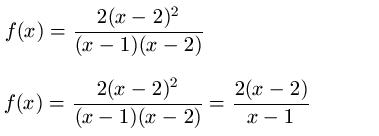
Links:

• Definitionslücke, Pole, Nullstelle Aufgabe
• Zur Mathematik-Übersicht