Division bzw. Dividieren von Zahlen

Das Dividieren gehört zu den Grundrechenarten der Mathematik. Die Division ist die Umkehrung der Multiplikation. Wie sie funktioniert und warum man sie braucht, erklären wir in diesem Artikel.

Wozu braucht man die Division? Starten wir mit einer ganz einfachen Erklärung. 6 Bälle sollen gleichmäßig auf 2 Körbe verteilt werden. Wie viele Bälle sind in jedem Korb? Dies kann man für so ein einfaches Beispiel natürlich sehr einfach ausprobieren. So landen am Ende jeweils 3 Bälle in jedem Korb.

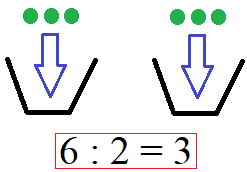
So eine Rechenaufgabe kann man mit einer Division darstellen. 6 Bälle auf 2 Körbe verteilt macht 3 Bälle in jedem Korb.

• Aufgabe: 6 : 2 = 3
• Gesprochen: 6 durch 2 gleich 3.

Dividieren Begriffe und Beispiele

Mathematiker haben Begriffe für die einzelnen Teile einer Division. Die erste Zahl vorne wird als Dividend bezeichnet. Nach dem Geteiltzeichen folgt der Divisor. Das Ergebnis wird hinter ein Istgleich-Zeichen geschrieben und als Quotient bezeichnet.

Wie kann jeder Schüler (oder auch Erwachsene) die Division am einfachsten lernen? Hilfreich ist dabei sich klar zu machen, dass die Division die Umkehrung der Multiplikation ist. Wenn du noch nicht multiplizieren kannst, solltest du erst einen Blick auf unseren Artikel Multiplikation werfen. Die folgenden Beispiele dürfen dir dann die Division verständlicher machen:

• 20 : 5 = 4, denn 4 · 5 = 20
• 12 : 4 = 3, denn 3 · 4 = 12
• 10 : 2 = 5, denn 5 · 2 = 10
• 18 : 6 = 3, denn 3 · 6 = 18
• 15 : 5 = 3, denn 3 · 5 = 15
• 24 : 6 = 4, denn 4 · 6 = 24

Wie man sehen kann, muss man eine Zahl suchen, die man mit dem Divisor multipliziert und damit den Dividend herausbekommt. Nicht jede Division geht auf. Dazu jedoch mehr im nächsten Abschnitt.

Divisionen mit Rest

Die eben gezeigten Beispiele hatten alle eins gemeinsam: Es gab keinen so genannten "Rest". Wie entsteht ein Rest? Nehmen wir nicht wie im Eingangsbeispiel 6 Bälle sondern 7 Bälle und teilen diese auf 2 Körbe gleichmäßig auf. So landen 3 Bälle in jedem Korb. Aber 1 Ball bleibt übrig. Dies ist unser Rest.

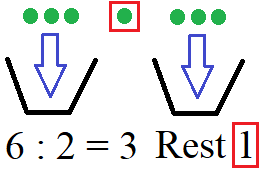
Um dies zu verstehen, noch einmal ein kleines Beispiel.

• 22 : 5 = 4 Rest 2

Wieso ist das so? Nun eigentlich ganz einfach: 5 · 4 = 20. Und 5 · 5 = 25. Das erste Ergebnis wäre zu klein, das zweite ist zu groß. Also geht man her und nimmt das erste Ergebnis: 5 · 4 = 20. Um aber auf die 22 zu kommen, muss noch die Zahl 2 addiert werden. Wem das jetzt noch nicht einleuchtet, schaut am besten gleich auf die nächsten Beispiele.

Weitere Beispiele Division:

• 17 : 3 = 5 Rest 2, denn 5 · 3 = 15. Fehlen noch 2 bis zur 17.
• 22 : 6 = 3 Rest 4, denn 3 · 6 = 18. Fehlen noch 4 bis zur 22.
• 13 : 5 = 2 Rest 3, denn 2 · 5 = 10. Fehlen noch 3 bis zur 13.
• 27 : 4 = 6 Rest 3, denn 6 · 4 = 24. Fehlen noch 3 bis zur 27.
• 31 : 5 = 6 Rest 1, denn 6 · 5 = 30. Fehlt noch 1 bis zur 31.

Division Eigenschaften, weiterführende Inhalte

Bevor wir mit dem Stoff weitermachen, möchte ich zunächst noch einmal kurz auf einige Eigenarten der Division hinweisen.

• Die Division ist die Umkehrung der Multiplikation.
• Die Division ist nicht kommutativ: Das bedeutet, dass 24 : 3 nicht das selbe Ergebnis liefert wie 3 : 24. Die Zahlen dürfen also nicht vertauscht werden!
• Ist der Dividend Null, ist das Ergebnis immer Null. Beispiel: 0 : 25 = 0
• Durch Null darf nie geteilt werden ! 25 : 0 darf nicht gerechnet werden!

Übungsaufgaben, schriftliche Division:

Bislang haben wir mit relativ kleinen Dividenden (die Zahl am Anfang) gearbeitet. Das ist leider nicht immer so. Wie man mit größeren Zahlen rechnet, behandeln wir auf den folgenden Seiten. Das Thema nennt sich dann schriftliche Division. Bevor ihr dieses jedoch lest, solltet ihr zunächst die Übungsaufgaben zu diesem Artikel erledigen.

• Division Aufgaben
• Schriftliche Division
• Zur Mathematik-Übersicht