E-Funktion integrieren

In diesem Artikel geht es um die Integration von E-Funktionen. Dies wird durch einige Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

In diesem Artikel geht es um die Integration von E-Funktionen. Dazu sollte ihr wissen, was eine E-Funktion ist und schon einige Integrationsregeln kennen. Wer die folgenden Themen noch nicht kennt, der sollte diese erst einmal durchlesen. Alle anderen können gleich mit den nächsten Abschnitten weitermachen.

• E-Funktion
• Partielle Integration
• Integration durch Substitution

Erklärung als Video:
Dieses Thema liegt auch als Video vor. In diesem werden typische Aufgabenstellungen, Beispiele und Herleitungen vorgestellt. Per Button kann auch in den Vollbildmodus gewechselt werden. Das Video ist auch direkt in der Sektion E-Funktion integrieren Video aufrufbar. Bei Abspielproblemen hilft der Artikel Video Probleme.

Integration E-Funktion mit Beispiele

Sehen wir uns nun einige Beispiele zur Integration von E-Funktionen an. Wir starten dabei mit sehr einfachen Funktionen und steigern uns dann Stück für Stück.

Beispiel 1:

Zunächst soll die Funktion f(x) integriert werden. Aus der Formelsammlung kann man entnehmen, dass wenn man f(x) = e^x integriert man F(x) = e^x + C erhält.

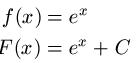
Beispiel 2:

Gegeben sei die Funktion f(x) = 2e^x. Auch hier soll die Stammfunktion gefunden werden. Dabei bleibt die Zahl 2 vor e^x erhalten. Kontrolle: Leitet man 2e^x + C wieder ab, so erhält man wieder 2e^x.

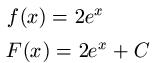
Beispiel 3:

Die nächste Funktion lautet f(x) = x · e^x. Wie man hier sehen kann, liegt ein Produkt vor. Heißt wir müssen die Partielle Integration - oft auch Produktintegration - anwenden. Dazu legen wir zunächst u und v' fest und bilden dann u' und v. Damit gehen wir in die Formel für die Partielle Integration und setzen ein. Wir erhalten F(x) = x · e^x - e^x + C.

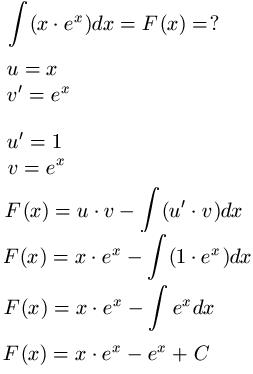
Beispiel 4:

Die nächste Funktion ist etwas komplizierter. Um hier eine Integration durchzuführen muss die Integration durch Substitution verwendet werden. Daher setzen wir z = 0,5x - 4, leiten dies ab und stellen nach dx um. Damit gehen wir in die Ausgangsfunktion, ersetzen also 0,5x - 4 durch z und dx ersetzen wir mit dz : 0,5. Die 0,5 ziehen wir nach vorne ( 1 : 0,5 = 2 ). Damit erhalten wir F(x) = 2e^{_{0,5x - 4}} + C.

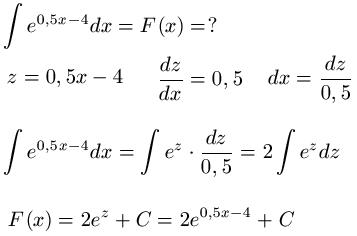
Links:

• Zur Mathematik-Übersicht