Integration durch Substitution

Mit der Integration durch Substitution befassen wir uns in diesem Artikel. Dabei wird erklärt, warum man die Integration durch Substitution benötigt und es werden Beispiele vorgerechnet. Dieser Artikel gehört zu unserem Bereich Mathematik.

In der Mathematik und in der Technik gibt es oftmals Integrale, die nicht durch einfache Integrationsregeln zu lösen sind. Für solche Fälle muss man sich komplexerer Verfahren bedienen. Eines dieser Verfahren wird als Integration durch Substitution bezeichnet und soll in diesem Artikel gezeigt werden. Noch ein Hinweis: Wer noch keine Ahnung von der Integration hat, dem empfehle ich zunächst die folgenden Artikel zu lesen. Alle anderen können gleich mit der Integration durch Substitution loslegen.

• Integration Grundlagen
• Potenzregel + Summenregel
• Produktintegration
• Integration zur Flächenberechnung

Integration durch Substitution Erklärung

Klären wir zunächst, was man unter der Substitution überhaupt versteht: Unter Substitution versteht man allgemein das Ersetzen eines Terms durch einen anderen. Und genau das tun wir nun um eine Integration durchzuführen. Ich zeige dies gleich durch das Vorrechnen einiger Beispiele. Zunächst jedoch die allgemeine Vorgehensweise:

1. Substitution, Ableitung und Umstellen
2. Substitution bei der Integralaufgabe durchführen
3. Integral lösen
4. Rücksubstitution durchführen

Beispiele zur Substitution bei der Integration

Anhand dieser vier Punkte sollen nun einige Beispiele zur Integration durch Substitution vorgerechnet werden. Denn Beispiele verdeutlichen die Vorgehensweise in der Regel am besten.

Beispiel 1: Im ersten Beispiel soll ein Bruch integriert werden. Dabei halten wir uns an den 4-Punkte-Plan weiter oben. Im Schritt 1 substituieren wir den Nenner. Im Anschluss leiten wir ab und stellen nach dx um.  In Schritt 2.) setzen wir für 5x - 7 nun z ein und für dx setzen wir dz durch 5 ein. In Schritt Nr. 3 geht es dann darum die Integration durchzuführen. Und im letzten Schritt führen wir die Rücksubstitution durch.

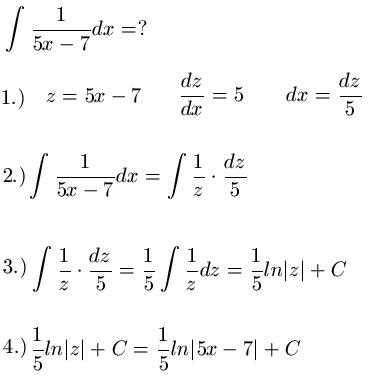
Beispiel 2: Im zweiten Beispiel zur Integration durch Substitution geht es darum eine Sinus-Funktion zu integrieren. Die Vorgehensweise sieht dabei aus wie im ersten Beispiel: Wir führen in Schritt 1.) zunächst eine Substitution durch, leiten ab und stellen nach dx um. Im Schritt 2.) setzen wir für 3 - 7x nun z ein und für dx nun dz durch -7. Im dritten Schritt geht es nun darum das Integral zu lösen um im letzten Schritt wird die Rücksubstitution durchgezogen.

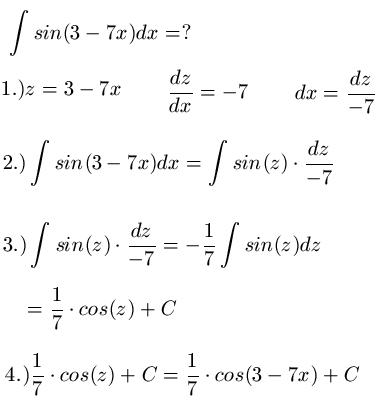
Beispiel 3: Im Beispiel Nr. 3 soll nun eine Fläche berechnet werden. Auch hier geht es zunächst erst einmal darum das Integral durch Einsatz von Substitution zu lösen. Nach der Rücksubstitution in Schritt 4.) geht es im Schritt 5.) dann um die Berechnung der Fläche. Also die obere und untere Grenze jeweils einsetzen, ausrechnen und die Differenz bilden. So wie man das bei der Flächenberechnung ( bei der Integration ) eben macht.

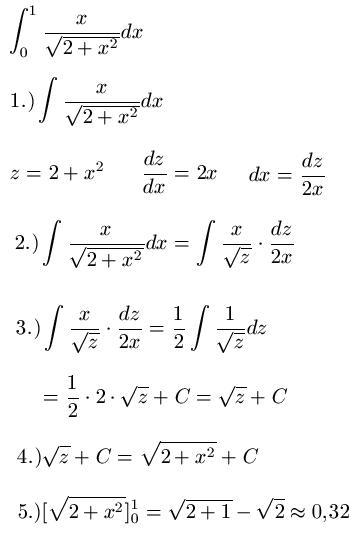
Links:

• Aufgaben / Übungen zur Integration durch Substitution
• Zur Integrations-Übersicht
• Zur Mathematik-Übersicht