Extremstelle berechnen

Wie kann man eine Extremstelle berechnen? Genau dies sehen wir uns mit einem Hochpunkt und einem Tiefpunkt bei einem Beispiel an. Zunächst gibt es jedoch einen Plan, wie man allgemein mit so einer Aufgabe umgeht. Dieser Artikel gehört zu unserem Bereich Mathematik.

Wir sehen uns gleich einmal an, wie man eine Extremstelle berechnen kann. Dazu rechne ich ein Beispiel vor. Zunächst gibt es jedoch einen allgemeinen Plan, wie man an solch eine Aufgabe rangehen kann.

Allgemeine Vorgehensweise:

Um die Extremstelle oder die Extremstellen bei einer Aufgabe zu berechnen geht man so vor:

1. Wir bilden die erste und zweite Ableitung der Funktion.
2. Wir setzen die erste Ableitung null um Kandidaten für Extremstellen zu finden.
3. Mit diesen Kandidaten gehen wir in die zweite Ableitung.
4. Damit finden wir die Minimumstelle oder Maximumstelle.
5. Wir können damit Tiefpunkt bzw. Hochpunkt berechnen.

Extremstelle berechnen: Beispiel

Wenden wir diese allgemeine Vorgehensweise auf ein Beispiel an. Ich rechne zunächst alles vor, im Anschluss wird die Rechnung noch einmal ausführlich erklärt.

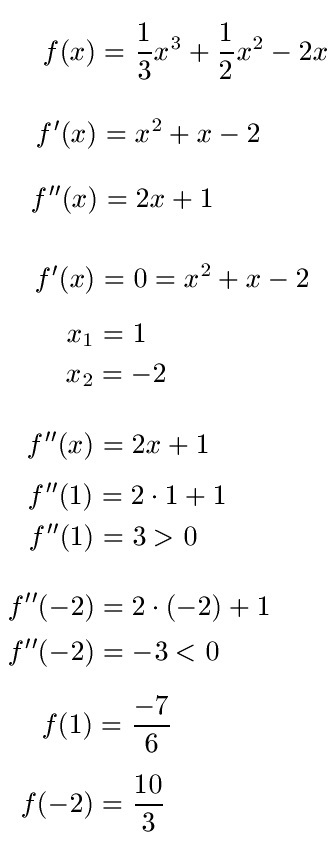
Gehen wir dies Stück für Stück einmal durch:

1. Wir haben die Funktion f(x) und bilden die 1. Ableitung und die 2. Ableitung. Wer hier noch Probleme hat sollte einmal in den Artikel Potenzregel und Summenregel reinsehen. Dort werden die entsprechenden Ableitungsregeln erklärt.
2. Wir setzen die erste Ableitung nun, also f'(x) = 0 und erhalten 0 = x² + x - 2. Dies ist eine quadratische Gleichung. So etwas löst man zum Beispiel mit der PQ-Formel. Wir erhalten damit x₁ = 1 und x₂ = -2. An diesen Stellen kann eine Extremstelle vorliegen.
3. Um dies zu überprüfen brauchen wir die zweite Ableitung. Wir nehmen daher f''(x) und setzen x = 1 und x = -2 ein.
4. Setzen wir in die zweite Ableitung x = 1 ein, dann erhalten wir 3 > 0. Bei x = 1 liegt daher eine Minimumstelle. Setzen wir in die zweite Ableitung x = - 2 ein, dann erhalten wir -3 < 0. Bei x = - 2 liegt daher eine Maximumstelle.
5. Wir wissen nun, dass die Extremstellen bei x₁ = 1 und x₂ = -2 liegen. Wir können damit noch die Extrempunkte ausrechnen. Dazu setzen wir in f(x) noch x = 1 ein und im Anschluss setzen wir in f(x) noch x = -2 ein. Damit erhalten wir f(1) = -7/6 und f(2) = 10/3. Wir wissen also Hochpunkt und Tiefpunkt damit. Die Minimumstelle liegt bei P_MIN (1;-7/6) und die Maximumstelle bei P_HOCH (-2;10/3).

Hinweise:

• Begriffe:Wer mit den Begriffen Extremstelle, Extremwert und Extrempunkt noch kämpft, der kann gerne auch einmal in den Artikel Unterschied Extremstelle, Extremwert und Extrempunkt reinsehen.
• Sattelpunkt und Wendepunkt: Außerdem bieten wir Inhalte noch zum Sattelpunkt berechnen und Wendepunkt berechnen an.
• Ableitung: Mit den Ableitungsregeln befassen wir uns im Artikel Ableitungsregeln.

Weitere Links:

• Zur Mathematik-Übersicht