Sattelpunkt berechnen

Ein Sattelpunkt ist ein Spezialfall eines Wendepunktes. Was es damit genau auf sich hat und wie man diesen Punkt berechnet, lernt ihr in diesem Artikel der Mathematik.

Im nun Folgenden gehen wir näher auf den Begriff des Sattelpunktes ein. Damit ihr diesen Artikel jedoch verstehen könnt, solltet ihr einige Vorkenntnisse mitbringen. Wem die folgenden Artikel noch gar nichts sagen, der möge sie bitte nachlesen. Alle anderen können gleich mit dem Sattelpunkt starten.

• Fakotorregel und Summenregel
• Tabelle von Ableitungen
• Erste und zweite Ableitung
• Extremwerte: Hochpunkt und Tiefpunkt
• Wendepunkt berechnen

Was ist ein Sattelpunkt?

Erst einmal eine kurze Erinnerung: Ein Wendepunkt ist ein Punkt auf einem Funktionsgraphen, an welchem der Graph sein Krümmungsverhalten ändert. Ein Graph wechselt hier entweder von einer Rechts- in eine Linkskurve oder umgekehrt. In der folgenden Grafik wurde ein solcher Wendepunkt eingezeichnet.

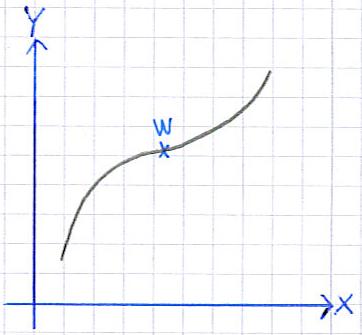
Ein Wendepunkt mit waagrechter Tangente wird als Sattelpunkt oder auch Terrassenpunkt bezeichnet. Die folgende Grafik zeigt euch einen Sattelpunkt:

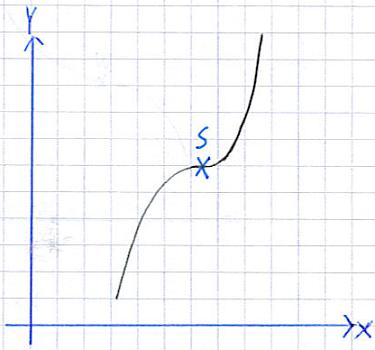
Sattelpunkt ermitteln

Nun stellt sich natürlich die Frage: Wie berechne ich einen Sattelpunkt? Dazu bedient man sich wie auch beim Hochpunkt bzw. Tiefpunkt der Differentialrechnung. Die hinreichende Bedingung für einen Sattelpunkt lautet:

• f'(x₀) = 0
• f''(x₀) = 0
• f'''(x₀ ) ≠ 0

Praktische Vorgehensweise:

Um eine Funktion auf Sattelpunkte hin zu untersuchen, führen wir die folgenden Schritte durch:

1. Wir leiten die Funktion f(x) dreimal ab.
2. Wir setzen die erste Ableitung Null
3. Wir setzen die zweite Ableitung Null
4. Sofern möglich, setzen wir diesen X-Wert in die dritte Ableitung ein
5. f'''(x) muss dann ungleich Null sein
6. Der X-Wert wird in f(x) eingesetzt, um den zugehörigen Y-Wert zu bestimmen

Beispiel:

Das folgende Beispiel demonstriert die Berechnung des Sattelpunktes:

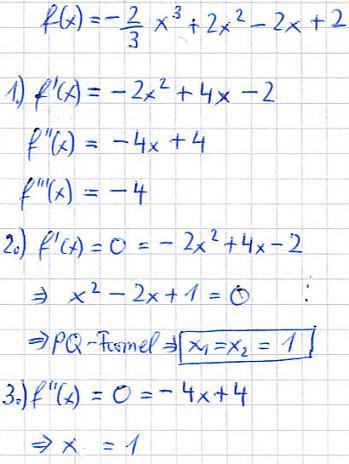
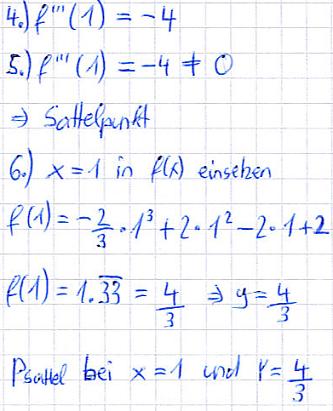
Links:

• Zur Ableitung-Übersicht
• Zur Mathematik-Übersicht