Wie man den Flächeninhalt eines Rechtecks berechnet, lernst du in diesem Artikel. Du bekommst Formeln für die Berechnung des Flächeninhaltes vorgestellt, sowohl mit den Seitenlängen als auch mit dem Umfang des Rechtecks. Mit einigen Beispielen lernst du sehr einfach wie die Flächenberechnung funktioniert. Die Inhalte liegen als Text und als Video vor.
Unter einem Rechteck versteht man ein Viereck mit 4 Seiten. Die gegenüberliegenden Seiten sind jeweils gleich lang und werden meistens mit a (hier rot) und b (hier blau) bezeichnet.

Der Flächeninhalt eines Rechtecks gibt an, wie groß das Rechteck ist. In Formeln wird der Flächeninhalt mit "A" abgekürzt. In der Grafik ist die Fläche in gelb dargestellt.
Flächeninhalt Rechteck: Formel
Im einfachsten Fall kann der Flächeninhalt berechnet werden, in dem die Länge des Rechtecks mit der Breite des Rechtecks multipliziert wird. Die Formel kann einfach verständlich als Text geschrieben werden.
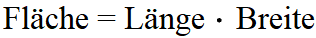
In der Mathematik wird jedoch in Formeln nicht mit Text gearbeitet, sondern mit Variablen (Buchstaben). Die Formel zur Berechnung des Flächeninhaltes sieht vor die Seitenlänge "a" des Rechtecks mit der Seitenlänge "b" zu multiplizieren um den Flächeninhalt "A" zu berechnen.
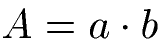
Auch mit dem Umfang des Rechtecks kann der Flächeninhalt berechnet werden. Für die Formel wird der Umfang "U" und eine der beiden Seitenlängen benötigt. Es folgt die Formel, ein Beispiel sehen wir uns weiter unten an.
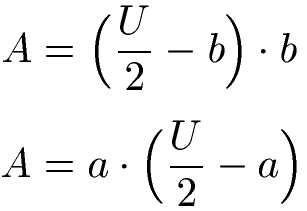
Hinweis: Die Seitenlängen müssen in der gleichen Einheit eingesetzt werden, zum Beispiel beide Seitenlängen in Zentimeter einsetzen oder beide Seitenlängen in Meter. Dies gilt auch wenn mit dem Umfang gerechnet wird. Am Ende des Artikels findest du noch Hilfen zur Umrechnung, falls verschiedene Längeneinheiten verwendet werden.
Beispiel: Rechteck Flächeninhalt berechnen
Ein Rechteck hat eine Länge von 4 Metern und eine Breite von 3 Metern. Wie groß ist der Flächeninhalt des Rechtecks?
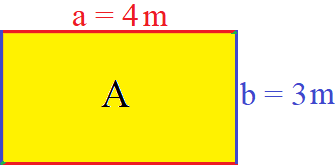
Die Länge und Breite des Rechtecks liegen in der gleichen Einheit vor, in diesem Fall sind beide Längeneinheiten in Metern angegeben. Wir müssen daher keine Umrechnung durchführen. In die Formel setzen wir a = 4 m und b = 3 m ein. Wir multiplizieren 4 mit 3 und erhalten 12. Außerdem multiplizieren wir Meter (m) mit Meter (m) und erhalten Quadratmeter (m2).
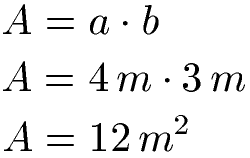
Ein Rechteck mit den Seitenlängen 4 Meter und 3 Meter hat einen Flächeninhalt von 12 Quadratmetern.
Flächeninhalt Rechteck zu Quadrat
Ein Rechteck zeichnet sich dadurch aus, dass die gegenüberliegenden Seiten des Rechtecks jeweils gleich lang sind. Von den 4 Seiten des Rechtecks sind somit je 2 gleich lang. Im Unterschied dazu sind bei einem Quadrat alle 4 Seiten gleich lang.
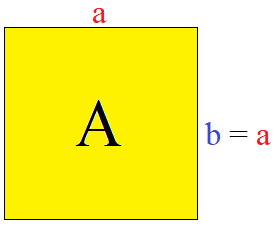
Der Flächeninhalt eines Quadrates berechnet sich ebenfalls mit Länge mal Breite. Da jedoch Länge und Breite gleich lang sind, kann auch einfach die Länge oder die Breite mit sich selbst multipliziert werden.
Quadrat Fläche Beispiel:
Als Beispiel nehmen wir ein Quadrat mit der Seitenlänge 2 Meter. Die Fläche des Quadrates ist Länge mal Breite. Da Breite und Länge gleich sind kann jedoch die Länge mit sich selbst multipliziert werden. Bei einer Seitenlänge von 2 Metern ist der Flächeninhalt des Quadrates 4 Quadratmeter.
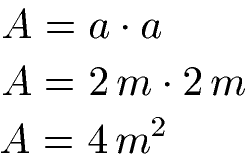
Dezimalzahlen und Einheiten Beispiel
Ein Rechteck hat Seitenlängen von 0,8 Meter und 270 Zentimeter. Wie groß ist der Flächeninhalt des Rechtecks? Zum besseren Verständnis der Aufgabe erst einmal eine kleine Grafik.
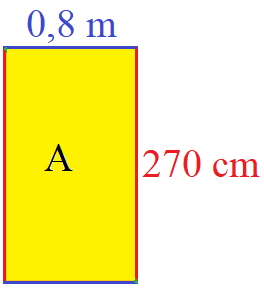
Länge und Breite des Rechtecks liegen in verschiedenen Längeneinheiten vor. Dies ist für die Berechnung der Fläche ungünstig. Daher rechnen wir beide Längenangaben auf die gleiche Längeneinheit um. Um nicht weiter mit Kommas rechnen zu müssen rechnen wir beide Seitenlängen auf Zentimeter um. Dazu multiplizieren wir die 0,8 mit 100 um von Meter auf Zentimeter umzurechnen.
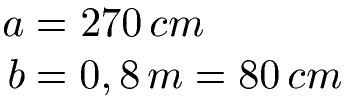
Im Anschluss multiplizieren wir Länge mit Breite und erhalten 21.600 Quadratzentimeter für die Größe des Rechtecks.
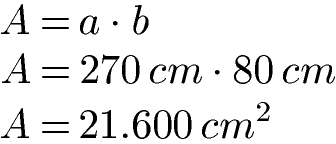
Solltest du Probleme haben 270 mit 80 zu multiplizieren kannst du entweder einen Taschenrechner einsetzen oder die schriftliche Multiplikation.
Flächeninhalt Rechteck mit Umfang berechnen
Der Flächeninhalt eines Rechtecks lässt sich mit dem Umfang berechnen. Dazu wird die Länge des Umfangs benötigt sowie eine weitere Seitenlänge. Die beiden Formeln um die Fläche zu berechnen und ein Beispiel sehen wir uns nun an.
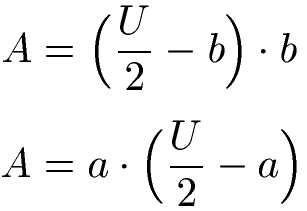
Fläche mit Umfang berechnen:
Der Umfang eines Rechtecks sei U = 20 Meter und die Seitenlänge b = 4 Meter. Wie groß ist der Flächeninhalt? Für die Berechnung setzen wir die Angaben in die Formel ein. Wir berechnen zunächst den Inhalt der Klammer, beginnend mit dem Bruch.
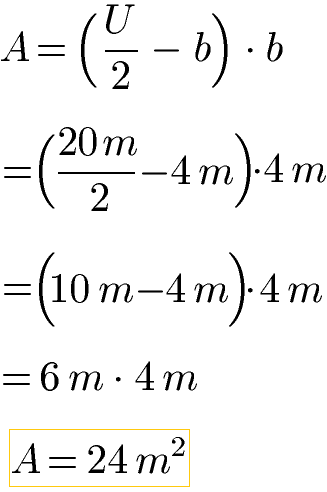
Weitere Beispiele und Erklärungen findest du noch unter Rechteck Umfang.
Einheiten und Längeneinheiten
Zur Berechnung der Fläche eines Rechtecks werden Zahlen mit Einheiten in die Formeln eingesetzt. Bei diesen Einheiten handelt es sich genauer gesagt um Längeneinheiten. Darunter fallen Kilometer, Meter, Dezimeter, Zentimeter und Millimeter. Diese Einheiten müssen manchmal umgerechnet werden. Die nächste Grafik zeigt die Umrechnungsfaktoren zwischen den einzelnen Längeneinheiten.
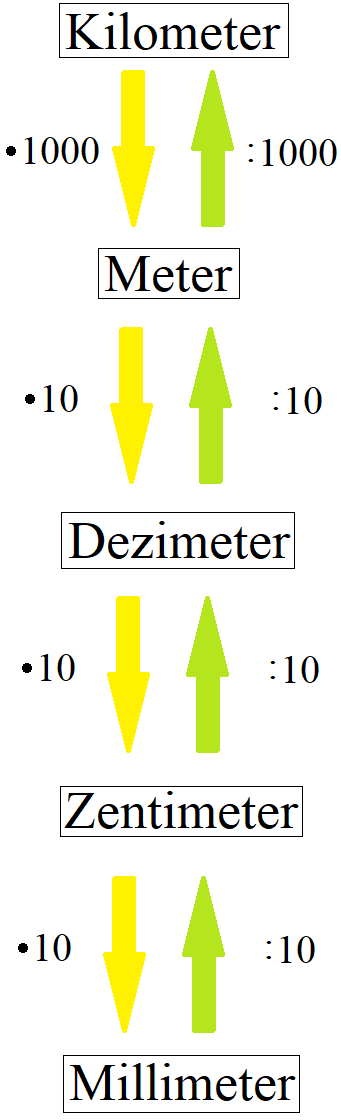
Mehr zu diesem Thema erfährst du mit Beispielen unter Einheiten umrechnen.
Links:
417 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: