Mit dem Hauptnenner befassen wir uns in diesem Artikel. Dabei erklären wir euch, was man unter dem Hauptnenner versteht und wie man diesen findet. Dieser Artikel gehört zum Bereich Mathematik.
Um Brüche addieren oder subtrahieren zu können, muss man diese auf einen gemeinsamen Nenner bringen. Hat man zwei Brüche, die jeweils schon gekürzt sind, so nennt man das kleinste gemeinsame Vielfache der beiden Nenner der Brüche den Hauptnenner. Im nun folgenden Artikel zeigen wir euch zwei Möglichkeiten, wie man einen gemeinsamen Nenner für einen Bruch findet.
Hauptnenner Möglichkeit 1: Teilerfremde Nenner
Sind die beiden Nenner teilerfremd, so ist der Hauptnenner das Produkt der beiden Nenner. Die beiden folgenden Beispiele verdeutlichen dies:
Beispiel 1:
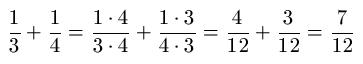
Der erste Bruch hat den Nenner 3, der zweite Bruch hat den Nenner 4. Aus diesem Grund wird der Zähler und der Nenner des ersten Bruchs mit 4 multipliziert und entsprechend der zweite Bruch mit 3. Die Multiplikationen werden berechnet und beide Brüche haben im Anschluss den gleichen Nenner. Nun ist die Addition der Brüche ganz einfach durch Addition der Zähler möglich. Der gemeinsame Nenner bleibt erhalten.
Beispiel 2:
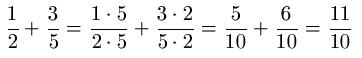
Der erste Bruch hat den Nenner 2, der zweite Bruch hat den Nenner 5. Aus diesem Grund wird der Zähler und der Nenner des ersten Bruchs mit 5 multipliziert und entsprechend der zweite Bruch mit 2. Die Multiplikationen werden berechnet und beide Brüche haben im Anschluss den gleichen Nenner. Nun ist die Addition der Brüche ganz einfach durch Addition der Zähler möglich. Der gemeinsame Nenner bleibt erhalten.
Wichtig: Die Multiplikation der beiden Nenner funktioniert immer, denn man erhält stets einen gemeinsamen Nenner. Nur dieser Nenner ist in vielen Fällen sehr groß. Aus diesem Grund kann man auch einen Hauptnenner unter Einsatz des kgV (kleinstes gemeinsames Vielfaches) suchen.
Hauptnenner finden mit kgV
Sehen wir uns zunächst einmal an, was das kleinste gemeinsame Vielfache, kurz kgV genannt, überhaupt ist: Wir untersuchen dabei zwei Zahlen, welche unseren beiden Nennern entsprechen. Dabei wird die jeweilige Zahl mit 2, 3, 4 etc. multipliziert und in einer Reihe aufgeschrieben. Dann wird nachgesehen, wo die kleinste gemeinsame Zahl zu finden ist.
Beispiel: (kgV von 6 und 18):
- Vielfache von 6: 6, 12, 18, 24....
- Vielfache von 18: 18, 36, 54....
- Kleinste gemeinsame Zahl ist somit die 18.
Beispiel: (kgV von 12 und 18):
- Vielfache von 12: 12, 24, 36, 48, 60 ....
- Vielfache von 18: 18, 36, 54, 72, 90 ...
- Kleinste gemeinsame Zahl ist somit die 36.
Mit dem Wissen zum kgV und dem Beispiel zum kgV von 12 und 18 berechnen wir nun das folgende Beispiel:
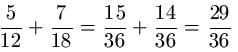
Zu den Zahlen 12 und 18 haben wir das kgV = 36 ermittelt. Wir multiplizieren den ersten Bruch mit 3, denn 12 · 3 = 36 und den zweiten Bruch mit 2, denn 18 · 2 = 36. Die beiden Brüche werden zuletzt addiert.
Weitere Links:
243 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
