Hessesche Normalform

Mit der Hesseschen Normalform befassen wir uns in diesem Artikel. Dabei erklären wir euch anhand von Beispielen, wie man die Hessesche Normalform bildet. Dieser Artikel gehört zum Bereich Mathematik.

Die hessesche Normalform ist in der analytischen Geometrie eine Gleichung, die eine Ebene  beschreibt und hauptsächlich für Abstandsberechnungen verwendet wird. Leider werden einige Grundkenntnisse benötigt, um diesen Artikel gut zu verstehen. Wer mit den folgenden Themen noch Probleme hat, der sollte diese erst einmal kurz nachlesen:

• Lineare Gleichungssysteme
• Kreuzprodukt / Vektorprodukt
• Betrag eines Vektors

Hessesche Normalform bestimmen

In diesem Abschnitt zeigen wir euch, wie man von einer Ebene in Koordinatenform zur Hesseschen Normalform kommt.  Zunächst folgt ein Beispiel, welches im Anschluss erklärt wird:

Beispiel 1:

Gegeben sei die Gleichung einer Ebene mit 3x - 4y + 2z = 6.  Ziel ist es, die Hessesche Normalform zu ermitteln.

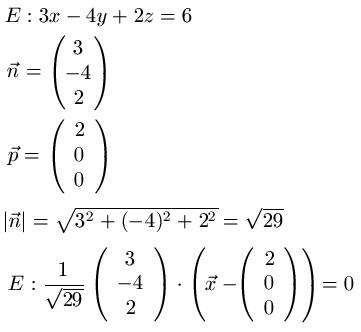
Aus der Ebenengleichung lesen wir den Normalenvektor "n" ab. Zu dem wählen wir uns einen Ortsvektor für einen beliebigen Punkt ( 3 · 2 -4 · 0 + 2 · 0 = 6 ). Im Anschluss bilden wir den Betrag des Normalenvektors. Als Letztes bilden wir die Hessesche Normalform.

Beispiel 2:

Gegeben sei die Gleichung einer Ebene mit 3x -2y +5z +2 = 0.  Ziel ist es, die Hessesche Normalform zu ermitteln.

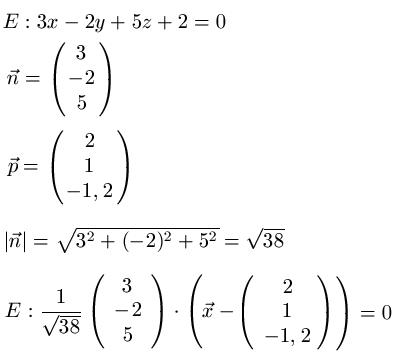
Aus der Ebenengleichung lesen wir den Normalenvektor "n" ab. Zu dem wählen wir uns einen Ortsvektor für einen beliebigen Punkt ( 3 · 2 + (-2) · 1 +5 · (-1,2) +2 = 0). Im Anschluss bilden wir den Betrag des Normalenvektors. Als Letztes bilden wir die Hessesche Normalform.

Die Hessesche Normalform in Koordinatenschreibweise erhalten wir, in dem wie die Ebenengleichung durch den Betrag des Normalenvektors dividieren:

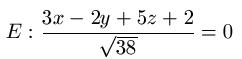
Links:

• Zur Mathematik-Übersicht