Partialdivision

Die Partialdivision - besser bekannt unter Polynomdivision - bereitet vielen Schülern und Schülerinnen große Probleme. Die folgenden Abschnitte sollen dabei helfen, euch die Partialdivision auf einfache Art und Weise verständlich zu machen. Dieser Artikel gehört zum Bereich Mathematik.

Die Partialdivision ist ein Verfahren der Mathematik, um Nullstellen von Polynomen zu berechnen. Die Berechnungsweise ähnelt der schriftlichen Division, die man bereits in der Grundschule kennen gelernt hat. Aus diesem Grund gehen wir im nun Folgenden erst einmal kurz auf die schriftliche Division ein und wenden dieses Wissen dann auf die Partialdivision an.

Beispiel: Schriftliche Division ( Erklärung unterhalb )

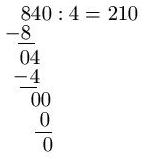
Lange ist es her, seit dem man das in der Grundschule gemacht hat. Also ... wie funktionierte das doch gleich nochmal? Hier die Vorgehensweise:

• Ziel ist es, die Lösung der Aufgabe 840 : 4 zu finden
• Die erste Zahl ist die 8. Teilt man 8 : 4 erhält man eine 2. Dies ist die erste Zahl für die Lösung
• Jetzt wieder zurück gerechnet: 2 · 4 = 8. Diese 8 wird unter die erste 8 am Anfang geschrieben.
• Jetzt werden die beiden Zahlen voneinander abgezogen, deshalb das "-" vor der unteren Zahl. 8 - 8 ergibt 0.
• Jetzt wird die nächste Zahl von oben runter geholt: Das ist eine 4.
• Jetzt wird wieder geteilt. 4 : 4 = 1. Die 1 wird wieder hingeschrieben
• Rückrechnen: 1 · 4 = 4. Die 4 wird wieder unter die andere 4 geschrieben
• Jetzt wird wieder abgezogen: 4 - 4 = 0.
• Die Null wird hingeschrieben. Von oben wird die nächste Zahl auch runter gezogen, ebenfalls eine 0.
• 0 : 4 = 0. Eine Null wird an das Ergebnis angehängt.
• Rückrechnung: 0 · 0 = 0 und 0 - 0 bleibt Null. Es gibt keine weiter Zahl von oben zu holen
• Es sind nur noch Nullen übrig. Damit ist dir Rechnung fertig.

Partialdivision Erklärung

Bei der Partialdivision dividiert man nun nicht zwei Zahlen, sondern ganze Terme bzw. Polynome. In der Mathematik bezeichnet der Begriff Term einen sinnvollen Ausdruck, der Zahlen, Variablen, Symbole ( für mathematische Verknüpfungen ) und Klammern enthalten kann. Um eine Partialdivision durchzuführen, benötigt man einen Term und eine Nullstelle dieses Terms. Um genau zu sein handelt es sich dabei um Polynome ( Was ist ein Polynom? ). Wir teilen ein Polynom durch ein anderes Polynom. Daher spricht man eben auch von Polynomdivision / Partialdivision.

Diese Nullstelle zu finden, ist oft recht schwierig. In der Schule gibt der Lehrer bzw. die Lehrerin die Nullstelle in aller Regel vor. Ist dies nicht der Fall, kann eine Nullstelle durch Raten oder numerische Verfahren gefunden werden. Für die nun folgenden Beispiele, gehen wir davon aus, dass eine Nullstelle bereits gegeben ist.

Partialdivision Beispiel 1:

Gegeben sei die Funktion y = f(x) = x³ - 2x² - 5x + 6. Durch probieren wurde eine Nullstelle bei x = 1 gefunden. Es soll nun die Partialdivision durchgeführt werden, um im Anschluss alle Nullstellen zu finden.

Lösung: Wir dividieren die Funktion y = f(x) durch ( x - 1 ). Dies sieht wie folgt aus:

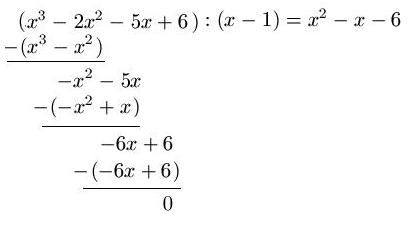
Wir berechnen hier zunächst x³ : x = x². Im Anschluss multiplizieren wird x² · ( x - 1 ) = x³ - x². Anschließend wird ( x³ - 2x² ) - ( x³ - x² ) berechnet. Danach beginnt das Spiel wieder von vorne, bis die Division komplett ist. Die Vorgehensweise entspricht der schriftlichen Division. Das Ergebnis der Partialdivision lautet x² - x - 6. Ob das Ergebnis stimmt, erfahren wir durch eine Probe:

Probe: ( x² - x - 6 ) · ( x - 1 ) = x³ - 2x² -5x + 6 // Die Lösung stimmt

Um nun noch die restlichen Nullstellen zu finden, wenden wir die PQ-Formel auf x² - x - 6 = 0 an und erhalten x₂ = 3 und x₃ = -2. Wir wissen somit, dass bei den x-Werten 1, 3 und -2 die Nullstellen liegen. Das Polynom kann man somit in seine Linearfaktoren zerfallen lassen: f(x) = ( x - 1 ) ( x - 3 ) ( x + 2 ). Auch hier führen wir die Probe durch:

Probe: ( x - 1 ) ( x - 3 ) ( x + 2 ) = x³ - 2x² - 5x + 6 // Die Lösung stimmt

Partialdivision Beispiel 2

Gegeben sei die Funktion y = f(x) = 3x³ - 10x² + 7x - 12. Eine Nullstelle bei x = 3 sei bekannt. Gesucht sind alle Nullstellen von f(x).

Lösung: Wir dividieren zunächst die Funktion f(x) durch ( x - 3 ). Dies sieht wie folgt aus:

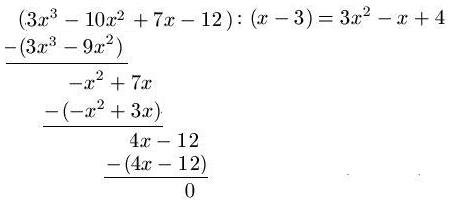
Auch hier berechnen wir Stück für Stück das Ergebnis. Zunächst wird 3x³ : ( x - 3 ) berechnet, das Ergebnis lautet 3x². Wir multiplizieren zurück: 3x² · ( x - 3 ) und erhalten 3x³ - 9x². Dann subtrahieren wir wieder und berechnen die Aufgabe im gewohnten Stil weiter. Das Ergebnis der Partialdivision lautet 3x² - x + 4. Wir führen eine Probe zur Sicherheit durch.

Probe: ( x - 3 ) ( 3x² -x + 4 ) = 3x³ - 10x² + 7x - 12

Um weitere Nullstellen zu finden, wenden wir auf 3x² - x + 4 = 0 die PQ-Formel an ( Wichtig: Dabei erst durch 3 teilen ). Bei der Anwendung der PQ-Formel erhält man eine negative Zahl unter der Wurzel. Damit endet die Rechnung ( für Schüler ) und die einzige Nullstelle liegt bei x = 3.

Um die Partialdivision wirklich zu erlernen, ist es sinnvoll zahlreiche Beispiele anzusehen und auch selbst Beispiele zu rechnen.

Links:

• Partialdivision Aufgaben / Übungen
• Zur Mathematik-Übersicht