Vielfache und Teiler bekommst du hier durch viele Beispiele erklärt. Den größten gemeinsamen Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) folgen im Anschluss. Passend dazu gibt es außerdem noch die Primzahlen und die Primfaktorzerlegung.
Starten wir mit den Vielfachen. Um die Vielfachen einer Zahl zu erhalten, multiplizieren wir diese Zahl mit den natürlichen Zahlen 1, 2, 3, 4, 5 und so weiter. Das Ergebnis dieser Multiplikationen sind die Vielfachen. Es folgen zahlreiche Beispiele zu den Vielfachen der Zahlen 2 bis 12, 24, 45, 75 und 111. Die Vielfachen sind jeweils rot eingerahmt.
Vielfache von 2:
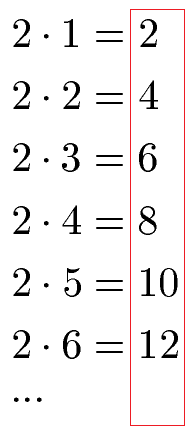
Vielfache von 3:
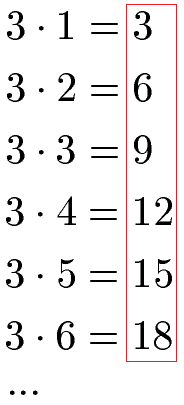
Vielfache von 4:

Vielfache von 5:

Vielfache von 6:
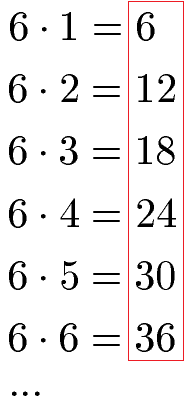
Vielfache von 7:

Vielfache von 8:

Vielfache von 9:

Vielfache von 10:

Vielfache von 11:

Vielfache von 12:

Vielfache von 24:

Vielfache von 45:

Vielfache von 75:
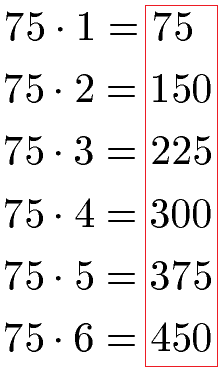
Vielfache von 111:

Teiler berechnen
Neben den Vielfachen interessiert man sich in der Mathematik oftmals auch für die Teiler einer Zahl. Für die ersten beiden Beispiele sollen die Teiler der Zahlen 4 und 5 berechnet. Wir teilen diese Zahlen jeweils durch die natürlichen Zahlen von 1 bis zu der entsprechenden Zahl. Teiler sind all die Zahlen, welche bei der Berechnung keinen Rest erzeugen.
Teiler von 4:
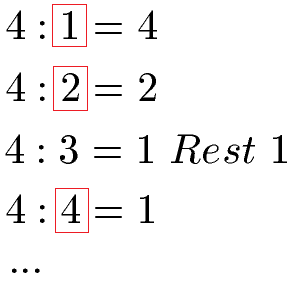
Die Teiler der Zahl 4 sind die Zahlen 1, 2 und 4. Die Zahl 3 ist kein Teiler, denn es entsteht ein Rest bei der Division.
Teiler von 5:
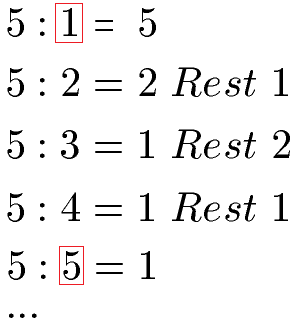
Die Teiler der Zahl 5 sind die Zahlen 1 und 5. Die Zahlen 2, 3 und 4 sind keine Teiler, denn es entsteht ein Rest bei der Division.
Teiler größerer Zahlen:
Insbesondere wenn die Zahlen größer werden macht das Suchen nach den Teilern mehr Arbeit. Eine erste Erleichterung ist es nur bis zur Hälfte der Ausgangszahl zu teilen. Zum Beispiel suchen wir für die 24 nur bis zur 12. Durch die Zahl selbst (24) kann natürlich ebenfalls geteilt werden.
Teiler bis 24:
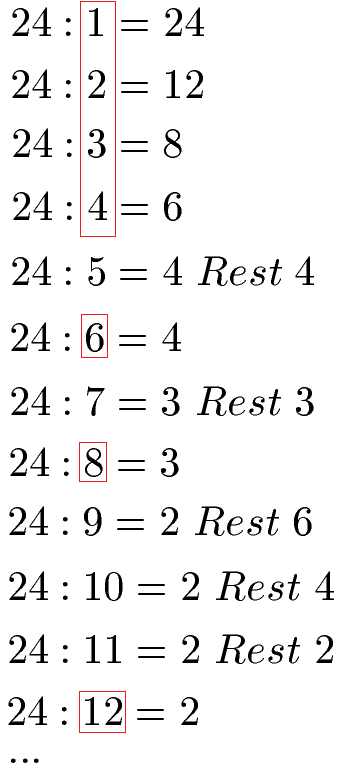
Die Teiler der Zahlen 24 sind damit 1, 2, 3, 4, 6, 8, 12 und die 24 selbst. In allen anderen Fällen entsteht ein Rest.
Teiler bis 36:
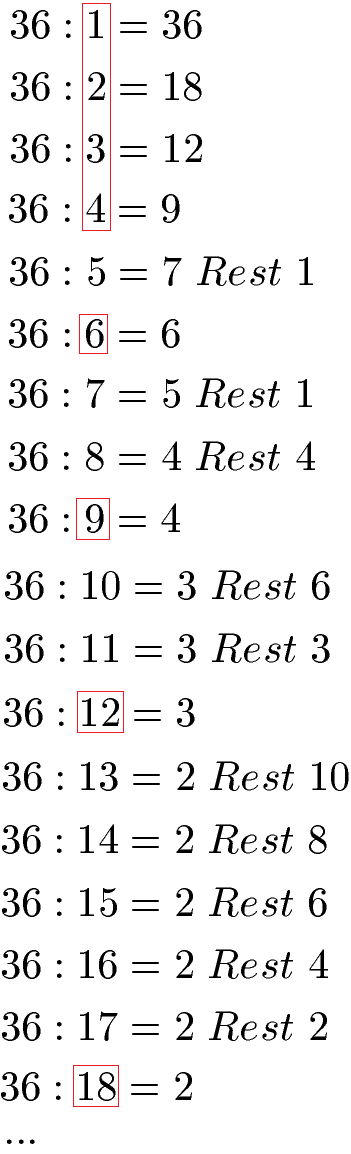
Teiler haben wir bei den Divisoren bei denen kein Rest entsteht. Die Teiler der Zahlen 36 sind damit die Zahlen 1, 2, 3, 4, 6, 9, 12, 18 und die 36 selbst.
Größter gemeinsamer Teiler (ggT)
In diesem Abschnitt beschäftigen wir uns mit dem größten gemeinsamen Teiler, kurz ggT genannt. Dabei werden zwei Zahlen "zerlegt" und untersucht, welche größtmöglichen Teiler beide haben. Auch das lässt sich am Besten anhand von Beispielen verstehen.
Beispiel 1 (Zahlen 6 und 12):
Wie lautet der größte gemeinsame Teiler der Zahlen 6 und 12? Lösung:
- Die Teiler von 6: 1, 2, 3, 6
- Die Teiler von 12: 1, 2, 3, 4, 6, 12
- Die Zahl 6 ist die größte Zahl, die bei beiden Teilern vorkommt.
Damit ist die Zahl 6 der größte gemeinsame Teiler von 6 und 12. Dies schreibt man in der Mathematik mit ggT(6;12) = 6.
Beispiel 2 (Zahlen 36 und 48):
Wie lautet der größte gemeinsame Teiler der Zahlen 36 und 48? Lösung:
- Teiler von 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
- Teiler von 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
- Die Zahl 12 ist die größte Zahl, die bei beiden Teilern vorkommt.
Damit ist die Zahl 12 der größte gemeinsame Teiler (ggT) der Zahlen 36 und 48. Dies schreibt man in der Mathematik mit ggT(36;48) = 12.
Noch einmal zum Mitdenken: Für beide Zahlen werden die Teiler gesucht. Dazu wird geprüft, durch welche Zahl sich teilen lässt, ohne dabei einen Rest (eine Kommazahl) zu erhalten. Sind alle Teiler gefunden, wird nachgesehen, welche die größte Zahl ist, die bei beiden Teilern zu finden ist.
Kleinstes gemeinsames Vielfaches (kgV)
Fehlt uns nun noch das kleinste gemeinsame Vielfache, kurz kgV genannt. Hier werden erneut zwei Zahlen betrachtet. Dabei wird die jeweilige Zahl mit 2, 3, 4 etc. multipliziert und in einer Reihe aufgeschrieben. Dann wird nachgesehen, wo die kleinste gemeinsame Zahl zu finden ist.
Beispiel 1 (kgV von 6 und 18):
- Vielfache von 6: 6, 12, 18, 24....
- Vielfache von 18: 18, 36, 54....
- Kleinste gemeinsame Zahl ist somit die 18. Damit ist kgV(6;18) = 18.
Beispiel 2 (kgV von 12 und 18):
- Vielfache von 12: 12, 24, 36, 48, 60 ....
- Vielfache von 18: 18, 36, 54, 72, 90 ...
- Kleinste gemeinsame Zahl ist somit die 36. Damit ist kgV(12;18) = 36.
Den meisten Schülern und Schülerinnern in der Schule ist zunächst nicht klar, warum man so Dinge wie Primzahlen, Primfaktorzerlegung oder auch Teiler und Vielfache von Zahlen benötigt. Die Antwort darauf lautet: Diese Dinge werden in zukünftigen Mathestunden verwendet.
So ist es zum Beispiel bei der Bruchrechnung sinnvoll, die Brüche zu kürzen. Und um dies zu schaffen, muss man wissen, welche gemeinsamen Teiler die Zahlen haben. Sich mit diesem Artikel zu beschäftigen, lohnt sich also vor allem dann, wenn man sich anschließend mit der Bruchrechnung nicht so schwer tun möchte.
Primzahlen und Primfaktorzerlegung
Eine Primzahl ist eine Zahl, die nur durch 1 oder durch sich selbst ohne Rest teilbar ist. So und diesen Satz von eben bitte 3-5 mal durchlesen und darüber nachdenken. Eine Primzahl hat damit nur zwei Teiler. Dies ist schon das gesamte Geheimnis hinter Primzahlen.
Nehmen wir ein kleines Beispiel zum Verdeutlichen: Die Zahl 11. Diese Zahl lässt sich nicht durch 2, 3, 4, 5, 6, 7, 8, 9, 10, 12 oder eine andere Zahl teilen, ohne dass ein Rest (Kommazahl) entsteht. Die Zahl 11 ist nur durch 1 und sich selbst - also 11 - teilbar. Damit ist die Zahl 11 eine Primzahl. Genauso wie die folgenden Zahlen:
Primzahlen: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 ....
Primfaktorzerlegung:
Die Primfaktorzerlegung dient dazu, eine Zahl in möglichst kleine Produkte zu verwandeln. Oder anders ausgedrückt: Eine Zahl in möglichst kleine Multiplikationen von Primzahlen zu zerlegen. Dies lässt sich am Besten anhand von Beispielen zeigen.
Beispiel 1:
- 24 = 2 · 12
- 24 = 2 · 2 · 6
- 24 = 2 · 2 · 2 · 3
- Die Zahlen 2 und 3 sind die Primzahlen
Beispiel 2:
- 90 = 2 · 45
- 90 = 2 · 5 · 9
- 90 = 2 · 5 · 3 · 3
- Die Zahlen 2, 3 und 5 sind die Primzahlen
Übungsaufgaben / Klausuraufgaben:
Das mit Teilern, Vielfachen etc. lässt sich sehr gut bei der Bruchrechnung üben, da dies genau dort angewendet wird. Wer üben möchte, schaut also am Besten in unserem Bruchrechnungs-Bereich einmal vorbei.
Links:
- Primfaktorzerlegung
- Kleinstes gemeinsames Vielfaches (kgV)
- Größter gemeinsamer Teiler (kgV)
- Zur Bruchrechnung
- Zur Mathematik-Übersicht
210 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: