kgV ▷ kleinstes gemeinsames Vielfaches berechnen

Das kleinste gemeinsame Vielfache - kurz kgV - ist die kleinste Zahl, die ein Vielfaches von zwei oder mehr Zahlen ist. Das kgV lässt sich über Zahlenreihen berechnen oder durch Primfaktorzerlegung. Du bekommst hier Beispiele und Erklärungen zum Finden des kgV für 2 Zahlen und für 3 Zahlen. Die Inhalte liegen als Text und als Video vor.

Für kleine Zahlen findest du das kleinste gemeinsame Vielfache sehr einfach: Bilde dazu nächst die Zahlenreihen mit Vielfachen. Dazu multiplizierst du die Ausgangszahlen mit 1, 2, 3, 4 und so weiter. Als Beispiel die Vielfachen der Zahlen 3 und 4:

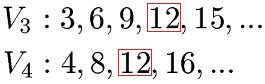
Aus den Vielfachen der beiden Zahlen suchen wir die kleinste Zahl, welche in beiden Zahlenreihen vorkommt. Für die Vielfachen von 3 und 4 ist dies die Zahl 12. Daher ist das kleinste gemeinsame Vielfache 12. Die mathematische Schreibweise dafür lautet kgV(3,4) = 12.

Im nächsten Beispiel soll das kgV von 6 und 7 berechnet werden. Dazu bilden wir die Vielfachen von 6 und 7 und suchen die kleinste Zahl, welche in beiden Zahlenreihen vorkommt.

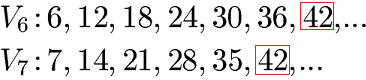
Das kleinste gemeinsame Vielfache von 6 und 7 lautet 42, kurz kgV(6,7) = 42. So einfach bleiben die Aufgaben jedoch nicht. Daher gehen wir jetzt an schwierigere Beispiele.

KgV mit Primfaktorzerlegung

Die Primfakorzerlegung hilft dabei das kleinste gemeinsame Vielfache für größere Zahlen oder für mehr als zwei Zahlen zu finden. Bei der Primfaktorzerlegung wird eine natürliche Zahl in Multiplikationen aus möglichst kleinen Zahlen zerlegt.

Als Beispiel soll die Primfaktorzerlegung der Zahlen 32 und 42 gezeigt werden und wie man dadurch das kgV findet. Eine 32 lässt sich in die Multiplikation aus 2 · 16 zerlegen. Diese 16 lässt sich weiter zerlegen bis wir am Ende die Gleichung 32 = 2 · 2 · 2 · 2 · 2 erhalten. Wir haben die Zahl 2 insgesamt 5 Mal. Daher können wir dies kurz als 2⁵ schreiben.

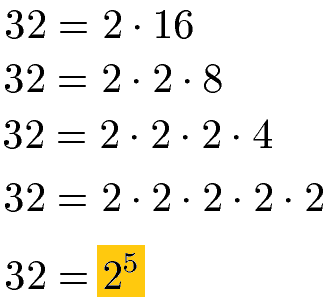
Die Zerlegung der 32 in möglichst kleine Zahlen bedeutet nichts anderes als ein Zerlegen in nur Primzahlen. Primzahlen sind Zahlen, die nur durch 1 und durch sich selbst teilbar sind. Solltest du Probleme haben Zahlen zu zerlegen wirf bitte noch einen Blick auf die Teilbarkeitsregeln oder auf die jetzt folgenden Beispiele.

Um das kleinste gemeinsame Vielfache von 32 und 42 zu finden zerlegen wir außerdem die 42 in eine Multiplikation aus Primzahlen. Die 42 kann in 2 · 21 zerlegt werden und die 21 in 3 · 7. Die Primzahlen sind dabei 2, 3 und 7. Da diese jeweils nur 1 Mal vorliegen erhalten wir in der Potenzschreibweise 2¹, 3¹ und 7¹.

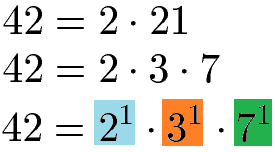
Das kleinste gemeinsame Vielfache (kgV) aus 32 und 42 finden wir, indem wir jede Basis aus beiden Zerlegungen suchen und jeweils den höchsten Exponenten nehmen. Bei der Zerlegung haben wir 2¹ und 2⁵ erhalten. Die 2⁵ ist größer als die 2¹, daher nehmen wir diese Potenz. Die Basis 3 und die Basis 7 gibt es nur bei einer der beiden Zerlegungen, daher nehmen wir diese ebenfalls mit 3¹ und 7¹. Mit diesen Potenzen können wir das kgV berechnen:

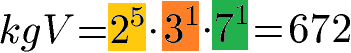
Das kleinste gemeinsame Vielfache der Zahlen 32 und 42 ist somit 672. Im nächsten Abschnitt sehen wir uns ein schwierigeres Beispiel an.

Kleinstes gemeinsames Vielfaches für 2 Zahlen

Das kleinste gemeinsame Vielfache für 2 Zahlen kann entweder über Vielfachenmengen oder über die Primfaktorzerlegung gefunden werden. Werden die Zahlen jedoch nur ein wenig größer, wird die Berechnung der Vielfachen jedoch sehr schnell aufwendig. Daher wird im nächsten Beispiel das Zerlegen in Primfaktoren noch einmal gezeigt.

Das kleinste gemeinsame Vielfache der Zahlen 36 und 92 soll berechnet werden. Dazu führen wir zunächst die Primfaktorzerlegung der 36 durch und bringen diese im Anschluss in die Potenzschreibweise:

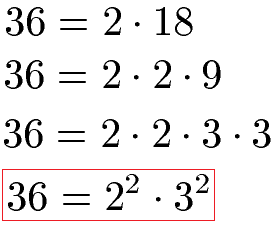
Die 92 wird ebenfalls in möglichst kleine Faktoren zerlegt und das Ergebnis als Potenz geschrieben.

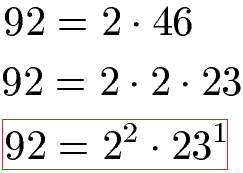
Um das kgV von 36 und 92 zu finden übernehmen wir die Primfaktorzerlegung in Potenzschreibweise für beide Zahlen. Die Basen lauten 2, 3 und 23. Wir übernehmen jeweils die Basen mit den höchsten Exponenten (Hochzahlen) und multiplizieren diese miteinander.

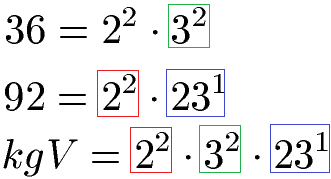
Das kgV können wir noch komplett ausrechnen und ergibt 828. Mathematisch ausgedrückt bedeutet dies kgV(36,92) = 828. Im nächsten Abschnitt sehen wir und das kleinste gemeinsame Vielfache für 3 Zahlen an.

Kleinstes gemeinsames Vielfaches für 3 Zahlen

Das kleinste gemeinsame Vielfache (kgV) für 3 Zahlen berechnen wir, indem wir für jede der Zahlen zunächst eine Primfaktorzerlegung durchführen. Als Beispiel soll das kgV von 88, 144 und 198 berechnet werden.

Zunächst führen wir eine Primfaktorzerlegung für die 88 durch und bringen das Ergebnis in die Potenzschreibweise:

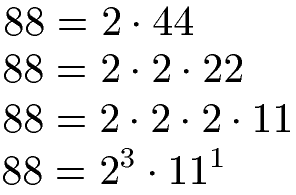
Die 144 wird ebenfalls in Primfaktoren zerlegt:

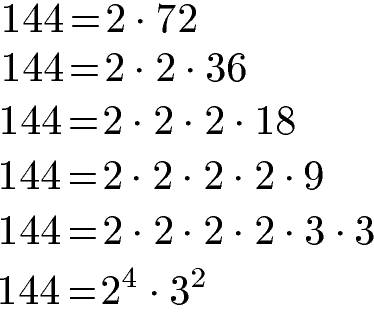
Als dritte Rechnung führen wir die Zerlegung in Primfaktoren für die 198 durch:

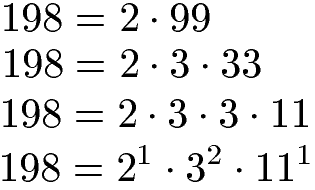
Aus den vorigen Berechnungen übernehmen wir die Primfaktorzerlegung in Potenzschreibweise für alle drei Zahlen. Wir übernehmen nun für die drei Basen (2, 3 und 11) jeweils die Potenz mit dem höchsten Exponenten. Bei 2¹, 2³ und 2⁴ ist dies 2⁴. Bei den Basen 3 und 11 sind die Exponenten (Hochzahlen) gleich. Die ausgewählten Potenzen werden miteinander multipliziert.

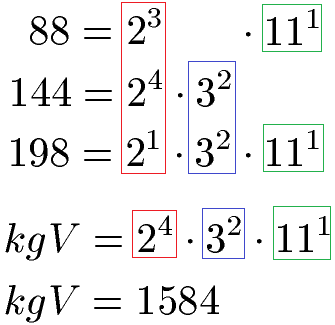
Das kleinste gemeinsame Vielfache benötigst du in Zukunft in der Bruchrechnung. Als nächstes empfehle ich dir das Thema größter gemeinsamer Teiler (ggT).