Primfaktorzerlegung ▷ Beispiele und Erklärung

Zur Primfaktorzerlegung bekommst du hier einfache Erklärungen und Beispiele vorgerechnet. Dabei rechne ich dir mehrere Aufgaben vor und erkläre was die Primfaktoren sind. Wozu du die Primfaktorzerlegung brauchst zeige ich dir mit dem kleinsten gemeinsamen Vielfachen (kgV) und dem größten gemeinsamen Teiler (ggT). Die Inhalte liegen als Text und als Video vor.

Die Primfaktorzerlegung dient dazu eine natürliche Zahl in ein Produkt aus Primzahlen zu verwandeln. Anders ausgedrückt: Wir zerlegen eine Zahl in eine Multiplikation aus möglichst kleinen Zahlen. Ein Beispiel:

Beispiel Primfaktorzerlegung 15:

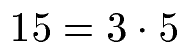
Dies ist noch ein sehr einfaches Beispiel. Daher sehen wir uns gleich noch schwierigere Beispiele zur Primfaktorzerlegung an. Auch solltest du verstehen wie man die Primfaktorzerlegung anwenden kann.

Primfaktor und Primfaktorzerlegung

Im Wort Primfaktorzerlegung kann man Primzahl und Faktor bereits erkennen. Zur Erinnerung:

• Primzahl: Eine Primzahl ist eine natürliche Zahl mit nur 2 Teilern: 1 und sich selbst. Die ersten Primzahlen lauten 2, 3, 5, 7, 11, 13, 17 und 19. In solche Primzahlen soll eine Zahl zerlegt werden.
• Faktor: Die Faktoren sind die Zahlen welche vor und nach einem Multiplikationszeichen stehen. Multipliziert man zwei oder mehr Faktoren miteinander ist das Ergebnis ein Produkt:

Begriffe Primfaktorzerlegung:

In diesem Beispiel sind 3 und 5 die Primzahlen und gleichzeitig die Faktoren. Aus diesem Grund werden solche Zahlen als Primfaktoren bezeichnet. Die Primfaktorzerlegung ist damit - wie der Name schon sagt - eine Zerlegung einer Zahl in Primfaktoren.

Um eine Primfaktorzerlegung durchzuführen, solltest du die Regeln der Teilbarkeit kennen. In welchen Fällen ist eine Zahl durch 2, durch 3 und so weiter teilbar. In den nächsten Beispielen stelle ich dir die jeweils verwendete Regel vor. Solltest du von diesem Thema noch gar keine Ahnung haben wirf bitte einen Blick in die Teilbarkeitsregeln.

Beispiele zur Primfaktorzerlegung

Starten wir einmal mit einer Primfaktorzerlegung bis 100. Als Beispiel soll die Zahl 48 vollständig in Primfaktoren zerlegt werden. Die 48 ist eine gerade Zahl, denn sie endet auf eine 8. Daher können wir 48 durch 2 teilen und in 2 · 24 zerlegen. Die 24 kann in 3 · 8 zerlegt werden und die 8 zerlegen wir erneut in 4 · 2 und die 4 in 2 · 2.

Hinweis: Die Primfaktorzerlegung kann verschieden durchgeführt werden. Am Ende dürfen jedoch nur Primzahlen übrig bleiben. Da wir 1 Mal die Zahl 3 und 4 Mal die Zahl 2 haben können wir das Ergebnis als Potenz schreiben

Primfaktorzerlegung der Zahl 48:

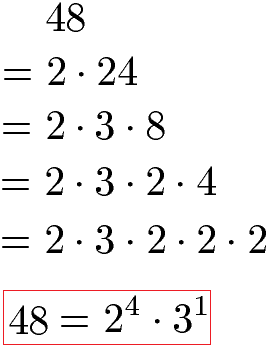
Um noch die Primfaktorzerlegung für eine ungerade Zahl zu zeigen sehen wir uns nun die Zerlegung der Zahl 225 an. Diese endet auf 5, ist daher durch 5 teilbar. Die 225 wird in 5 · 45 zerlegt. Die 45 endet erneut auf 5 und kann daher durch 5 ohne Rest geteilt werden. Wir zerlegen daher 45 in 5 · 9 und die 9 in 3 · 3. Dadurch ist die Primfaktorzerlegung vollständig. Wir schreiben das Ergebnis als Potenz, denn wir haben die Zahl 5 insgesamt 2 Mal und die Zahl 9 nur 1 Mal.

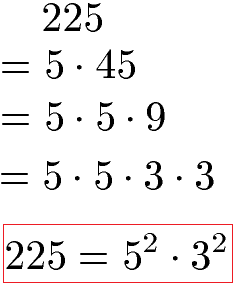
Anwendung Primfaktorzerlegung: ggT und kgV

Warum macht man eine Primfaktorzerlegung überhaupt? In der Schule werden zwei typische Anwendungen behandelt:

• Der größte gemeinsame Teiler, kurz ggT.
• Das kleinste gemeinsame Vielfache, kurz kgV.

Solltest du mit Teiler und Vielfachen nichts anfangen können wirf bitte erst einmal einen Blick auf Teiler und Vielfache. Ansonsten sehen wir uns jetzt eine Anleitung zur Berechnung von ggT und kgV an.

kgV und ggt für 32 und 42

Die Zahlen 32 und 42 sollen in Primfaktoren zerlegt werden. Mit den Primfaktoren soll das kleinste gemeinsame Vielfache (kgV) und der größte gemeinsame Teiler (ggT) gefunden werden.

Die Zahl 32 ist eine gerade Zahl, denn sind endet auf 2. Eine gerade Zahl kann durch 2 geteilt werden. Daher können wir aus 32 die Multiplikation 2 · 16 herleiten. Die 16 können wir zerlegen in 2 · 8 und die 8 können wir in 4 · 2 zerlegen sowie die 4 in 2 · 2. Wir erhalten 5 Mal die Zahl 2 als Primfaktorzerlegung. Dies kann durch eine Potenz abgekürzt werden mit 2⁵.

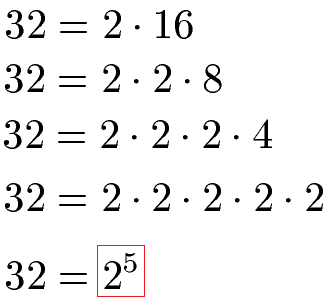
Die Zahl 42 ist eine gerade Zahl denn sie endet auf eine 2. Wir teilen daher 42 und 2 und erhalten die Zerlegung in 2 · 21. Die 21 kann ohne Rest durch 3 geteilt werden und wird daher in 3 · 7 zerlegt. Da 2, 3 und 7 Primzahlen sind ist die Zerlegung komplett. Wir bringen alles in die Potenzschreibweise.

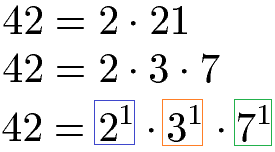
Als letzten Schritt sehen wir uns alle Potenzen an (farbig markiert).

Den größten gemeinsamen Teiler (ggT) finden wir, indem wir die Primfaktoren suchen welche in beiden Zerlegungen vorkommen und den kleinsten Exponenten haben. Die Basis 2 kommt bei 2⁵ und 2¹ vor. Wir nehmen den kleineren Exponenten, daher 2¹. Die Basen 3 und 7 kommen nur bei der Zerlegung von 42 vor, jedoch nicht bei der Zerlegung von 32 und fallen daher raus. Der ggT ist damit 2¹ = 2.

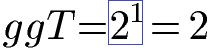
Das kleinste gemeinsame Vielfache (kgV) finden wir, indem wir jede Potenz aus beiden Zerlegungen nehmen und jeweils den höchsten Exponenten nehmen. Bei der Zerlegung haben wir 2¹ und 2⁵. 2⁵ ist größer, daher nehmen wir diese Potenz. Die Basis 3 und die Basis 7 gibt es nur bei einer Zerlegung, daher nehmen wir diese ebenfalls mit 3¹ und 7¹. Wir erhalten das kgV mit 2⁵ · 3¹ · 7¹ = 672.

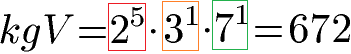
Ich empfehle dir als nächstes die Themen größter gemeinsame Teiler, kurz ggT und kleinstes gemeinsame Vielfache, kurz kgV.