Rotationsvolumen / Volumen Rotationskörper

In diesem Artikel geht es um das Rotationsvolumen bzw. das Volumen eines Rotationskörpers. Dies wird durch einige Beispiele gezeigt. Dieser Artikel gehört zu unserem Bereich Mathematik.

In diesem Artikel geht es um das Rotationsvolumen bzw. das Volumen eines Rotationskörpers. Dazu sollte ihr wissen, wie man Funktionen integriert und eventuell auch die Umkehrfunktion bildet. Wer die folgenden Themen noch nicht kennt, der sollte diese erst einmal durchlesen. Alle anderen können gleich mit den nächsten Abschnitten weitermachen.

• Integrationsregeln
• Umkehrfunktion

Erklärung als Video:
Dieses Thema liegt auch als Video vor. In diesem werden typische Aufgabenstellungen, ein allgemeiner Lösungsweg, Beispiele und Tipps vorgestellt. Per Button kann auch in den Vollbildmodus gewechselt werden. Das Video ist auch direkt in der Sektion Rotationsvolumen Video aufrufbar. Bei Abspielproblemen hilft der Artikel Video Probleme.

Was versteht man unter Rotationsvolumen?

In der Mathematik zeichnet man oftmals Funktionen in ein Koordinatensystem ein. Dreht man nun solch eine ebene Kurve um eine in der Kurvenebene liegende Achse erhält man einen Rotationskörper. Dazu zählen zum Beispiel Kugel, Kreiskegel oder auch Zylinder. Die nächste Grafik zeigt einen solchen Rotationskörper.

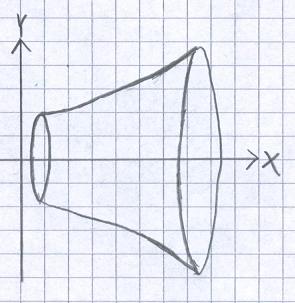
In diesem Fall kann man ein Rotationsvolumen bei der Drehung einer Kurve um die X-Achse sehen. Natürlich kann dies auch um die Y-Achse geschehen. Stellt sich jetzt noch die Frage: Wie berechne ich das Volumen eines Rotationskörpers? Genau darum drehen sich die nächsten Abschnitte.

Volumen Rotationskörper um die X-Achse

Bei Drehung einer Kurve um die X-Achse entsteht ein Rotationskörper mit dem Volumen V. Wichtig dabei ist, dass wir eine über dem Intervall [ a ; b ] stetige Funktion vorliegen haben. Ist dies der Fall, berechnet sich das Volumen wie folgt:

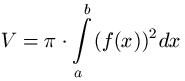
Beispiel 1:

Die Fläche unter dem Graphen der Funktion f(x) = x² rotiere im Intervall [ 0 ; 3 ] um die X-Achse. Das Volumen des Rotationskörper ist gesucht.

Lösung: Wir setzen f(x) in die Formel zur Berechnung des Volumens ein. Wir berechnen zunächst das Quadrat, integrieren dann und setzen die Grenze ein. Damit erhalten wir das Volumen.

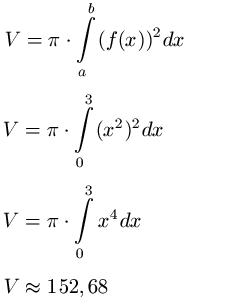
Volumen Rotationskörper um die Y-Achse

In diesem Abschnitt geht es um das Volumen eines Rotationskörpers um die Y-Achse. Hier liegt leider eine weitere Schwierigkeit vor. Denn meistens hat man eine Funktion der Form y = f(x) = ... irgendetwas... vor. Doch benötigt wird x = g(y), also die Umkehrfunktion. Wer noch keine Ahnung hat wie dies funktioniert schaut besser erst einmal in den Artikel Umkehrfunktion. Haben wir nun also x = g(y) gefunden, dann erhalten wir das Volumen mit der Formel:

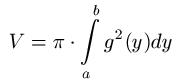
Beispiel 2:

Gegeben sei x = 2y. Im Intervall [ 0 ; 2 ] soll das Rotationsvolumen berechnet werden.

Lösung: Wir setzen x = 2y in die Formel ein und quadrieren. Dadurch erhalten wir nach dem Integral-Zeichen 4y²dy. Integrieren wir dies erhalten wir 4y³ : 3. Setzen wir noch die Grenzen ein ( und dann Pi vorne nicht vergessen ! ) ergibt sich ein Volumen von 33,51 VE.

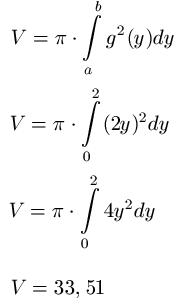
Links:

• Rotationsvolumen Aufgaben / Übungen
• Zur Mathematik-Übersicht