Fläche Kreis

Wie man die Fläche bei einem Kreis berechnet, lernt ihr in diesem Artikel. Wir liefern euch dazu die passenden Formeln sowie Beispiele zum besseren Verständnis. Auch Aufgaben / Übungen mit Lösungen haben wir im Angebot. Dieser Artikel gehört zu unserer Rubrik Mathematik.

Um die folgenden Beschreibungen zur Fläche eines Kreises zu verstehen, solltet ihr ein paar Vorkenntnisse aus dem Bereich der Mathematik mitbringen. Wem die folgenden Themen noch nichts sagen, der sollte diese erst einmal durchlesen. Alle anderen können gleich zur Berechnung der Kreisfläche weitergehen.

• Multiplikation von Zahlen
• Variablen und Formeln

Fläche eines Kreis berechnen

Wie berechnet man die Fläche eines Kreises? Mit genau dieser Frage beschäftigen wir uns im nun folgenden Abschnitt. Dazu schauen wir uns zunächst einen Kreis an. Wir erkennen: Der Kreis hat einen Mittelpunkt, die Begrenzung des Kreises ist von diesem Mittelpunkt immer den Abstand "r" entfernt. Die folgende Grafik zeigt euch dies:

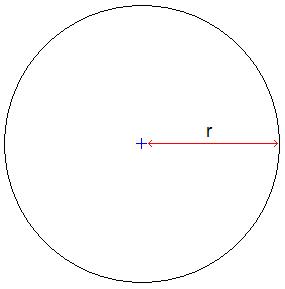
Neben dem Radius gibt es noch den so genannten Durchmesser. Der Durchmesser ist doppelt so groß wie der Radius. Darüber hinaus wird noch die so genannte Kreiszahl π ( gesprochen: pi ) benötigt. In der Schule setzt man für π in der Regel die Zahl 3,14159 ein.

Fläche Kreis Formeln:

Die beiden Formeln zur Berechnung des Flächeninhalts eines Kreises sehen wie folgt aus:

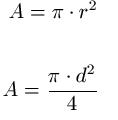
• "A" ist die Fläche des Kreises in Quadratmeter [ m² ]
• "π" ist die Kreiszahl 3,14159
• "r" ist der Radius des Kreises in Meter [ m ]
• "d" ist der Durchmesser des Kreises in Meter [ m ]

Hinweis:
Ihr bereitet euch auf eine Klausur vor? Ihr wollt das Rechnen am Kreis üben? Dann haben wir für euch entsprechende Aufgaben bzw. Übungen zur Verfügung. Alle mit Musterlösungen.

• Gleich zur ersten Aufgabe

Fläche Kreis: Beispiele

Im nun Folgenden möchten wir euch ein paar Beispiele zur Rechnung mit diesen beiden Formeln zeigen.

Beispiel 1:

Der Radius eines Kreises beträgt 0,34m. Mit beiden oben genannten Formeln soll die Fläche des Kreises berechnet werden.

Lösung: Den Radius setzen wir in die erste Gleichung ein und berechnen damit den Flächeninhalt. Um die zweite Formel nutzen zu können, muss der Radius zunächst verdoppelt werden, um den Durchmesser zu erhalten. Diesen Durchmesser setzen wir in die zweite Gleichung ein.

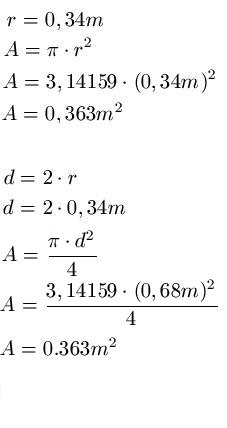
Beispiel 2:

Die Fläche eines Kreises beträgt 1,2m². Wir groß ist der Radius des Kreises?

Lösung: Wir stellen die Formel zur Berechnung vom Flächeninhalt um, damit wir direkt den Radius berechnen können. Danach setzen wir die Werte ein.

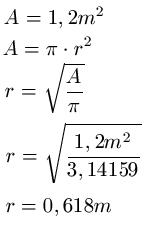
Links:

• Kreis Aufgaben / Übungen
• Zur Geometrie Übersicht
• Zur Mathematik-Übersicht