Geometrie: Gerade, Halbgerade und Strecke

In diesem Abschnitt beschäftigen wir uns mit Geraden, Halbgeraden und Strecken. Nach dem Durcharbeiten dieses Artikels solltet ihr die Unterschiede zwischen den einzelnen Begriffen der Geometrie kennen.

Beginnen wir zunächst mit einer Strecke. Um eine solche Strecke zu zeichnen, markiert man sich zwei Punkte auf dem Papier mit einem kleinen Kreuzchen. Anschließend legt man ein Lineal so an, dass man beide Punkte mit einer geraden Linie verbinden kann. Merke: Eine Strecke hat zwei Endpunkte. Die folgende Grafik zeigt euch, wie so eine Strecke aussieht.

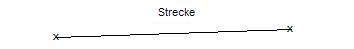
Geometrie: Halbgerade

Beschäftigen wir uns nun mit einer Halbgerade. Auch dazu gleich ein Merksatz: Eine Halbgerade ist eine Strecke, die einen Startpunkt hat, aber keinen Endpunkt. Für die Konstruktion bedeutet dies: Einen Startpunkt setzen (hier mit einem x markiert) und dann eine gerade Linie zeichnen. Da kein Endpunkt gesetzt wird, bedeutet dies: Die Linie geht ins Unendliche. Es folgt eine Grafik einer Halbgeraden.

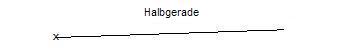
Geometrie: Eine Gerade zeichnen

Eine Strecke hat zwei Endpunkte, eine Halbgerade hat einen Endpunkt. Da bleibt nur noch "kein Endpunkt" für eine Gerade übrig. Und dem ist auch so. Hat eine Linie keine Endpunkte, ist sie eine Gerade. Die folgende Grafik verdeutlicht dies. Vergleicht diese einmal mit der Strecke und Halbgeraden.

Die Lage von Geraden zueinander

Als letztes haben wir gezeigt, was eine Gerade ist. Nun kann es natürlich passieren, dass man mehrere Geraden auf ein Blatt Papier (oder auf den Monitor eines PCs) zeichnet. Dabei können gewisse Dinge passieren bzw. man hat einige Bezeichnungen für besondere Zustände definiert. Klingt kompliziert, ist aber eigentlich ganz einfach:

• Zwei Geraden können sich höchstens in einem Punkt schneiden.
• Stehen zwei Geraden senkrecht aufeinander, so bilden diese einen rechten Winkel. Wir werden dies im Kapitel "Geodreieck und Winkel" noch genauer erklären.
• Sind zwei Geraden parallel zueinander, so schneiden diese sich niemals.

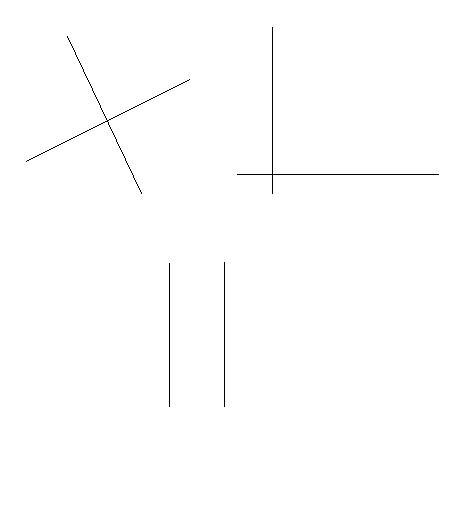
Betrachtet man zwei Geraden nicht auf einer Ebene, sondern in einem Raum, gibt es noch eine weitere Eigenschaft zu nennen:

• Zwei Geraden, die sich weder schneiden noch parallel sind, sind stets windschief.

Ihr solltet versuchen, euch die in diesem Artikel genannten Begriffe zu merken. Folgt danach dem Link zu den Übungsaufgaben. Versucht diese zunächst zu beantworten, ohne diesen Artikel dabei geöffnet zu haben. Seht erst anschließend in unsere Lösung. So könnt ihr überprüfen, ob ihr euch die Inhalte gemerkt habt.

• Zu den Übungsaufgaben "Gerade, Strecke und Halbgerade"
• Weiter zum Artikel "Winkel und Geodreieck"
• Zurück zur Geometrie Übersicht
• Zurück zur Mathematik-Übersicht