Mit der linearen Abhängigkeit von Vektoren befassen wir uns in diesem Artikel. Dabei geht es darum, was man unter lineare Abhängigkeit versteht und es wird anhand von Beispielen gezeigt, ob die Vektoren linear abhängig sind oder eben nicht. Dieser Artikel gehört zu unserem Bereich Mathematik.
Bevor wir mit der linearen Abhängigkeit von Vektoren beginnen, solltet ihr eure Vorkenntnisse kurz checken: Wem die folgenden Themen noch gar nichts sagen, der möge diese bitte erst nachlesen. Alle anderen können gleich mit dem nächsten Abschnitt weiter machen.
- Vektorrechnung: Addition, Subtraktion, Skalarprodukt
- Parallelität, Komplanarität und Kollinearität
- Gerade durch zwei Punkte
Lineare Abhängigkeit von zwei Vektoren
Warum prüft man zwei Vektoren auf lineare Abhängigkeit? Antwort: Zwei Geraden sind genau dann parallel zueinander, wenn die zugehörigen Richtungsvektoren linear abhängig sind. Wir finden also durch solch eine Untersuchung heraus, ob zwei Vektoren parallel sind. Dies kann man sowohl für Vektoren in der Ebene, als auch im Raum durchführen. Beides sehen wir uns nun an.
Vektoren in der Ebene:
Im nun Folgenden haben wir zwei Vektoren oder Geraden in der Ebene ( das erkennt man daran, dass nur zwei Zahlen "übereinander" stehen ). Es soll geprüft werden, ob diese jeweils linear abhängig sind oder nicht.
Beispiel 1:
Wir haben zwei Vektoren und sollen prüfen, ob diese linear abhängig sind. Dazu überprüfen wir, ob ein skalares Vielfaches vorliegt. Wir stellen ein lineares Gleichungssystem auf und sehen nach, ob bei der Auflösung nach der Variablen das gleiche Ergebnis raus kommt. Ist dies der Fall, sind die Vektoren linear abhängig.
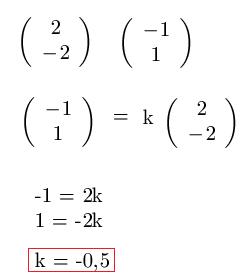
Für k = -0,5 werden beide Gleichungen erfüllt. Damit sind die beiden Vektoren linear abhängig - also parallel zueinander.
Beispiel 2:
Zwei weiteren Vektoren sollen auf lineare Abhängigkeit überprüft werden. Und wie man sehen kann, sind diese parallel, da k=1/3 beide Gleichungen erfüllt.
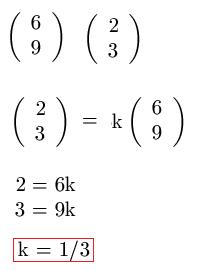
Beispiel 3:
Zwei weiteren Vektoren sollen auf lineare Abhängigkeit überprüft werden. Jedoch findet sich hier kein geeignetes k um beide Gleichungen zu erfüllen. Damit sind die Vektoren nicht parallel!
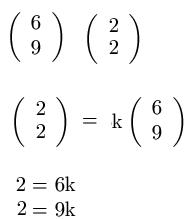
Beispiel 4:
Zwei Geraden sollen auf lineare Abhängigkeit überprüft werden. Dabei sehen wir uns auch hier die beiden Vektoren an und untersuchen diese daraufhin, ob ein ( skalares ) Vielfaches vorliegt. Dies ist für k = 1/3 der Fall. Damit sind die beiden Geraden parallel zueinander.
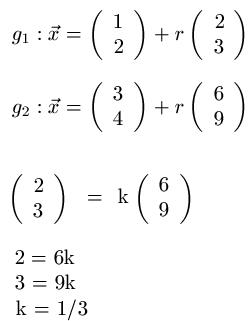
Vektoren im Raum:
Im nun Folgenden haben wir zwei Vektoren im Raum ( das erkennt man daran, dass drei Zahlen "übereinander" stehen ). Es soll geprüft werden, ob diese linear abhängig sind oder nicht. Dazu stellen wir wieder ein lineares Gleichungssystem auf. Wir haben dabei 3 Gleichungen mit je einer Variablen. Wie man sehen kann, wird jede Gleichung mit k = -0,5 erfüllt. Damit sind die Vektoren linear abhängig und parallel.
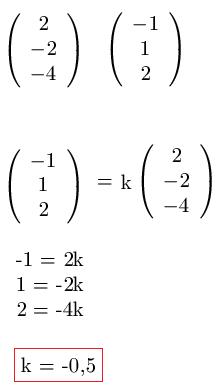
Lineare Abhängigkeit von drei Vektoren
In den folgenden Beispielen sehen wir uns nun an, ob 3 Vektoren linear abhängig sind oder eben nicht. Dabei gilt: Ist die Determinante D = 0, so sind die Vektoren linear abhängig. In diesem Fall sind die Vektoren komplanar, dass heißt sie liegen in einer gemeinsamen Ebene.
Beispiel 1:
Gegeben sind drei andere Vektoren. Die Frage lautet nun: Sind diese linear abhängig oder nicht? Dazu berechnen wir deren Determinante ( Artikeltipp: Determinante berechnen ).
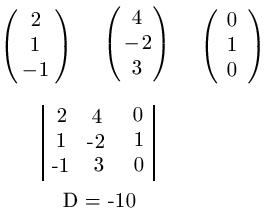
Die Determinante berechnet sich zu D = -10. Die Vektoren sind linear nicht abhängig ( = unabhängig ).
Noch ein Hinweis: Es gibt verschiedene Möglichkeiten die lineare Abhängigkeit zu prüfen. Nur einige davon wurden hier vorgestellt.
Links:
204 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige:
