Wichtige Rechengesetze der Mathematik werden hier ganz einfach erklärt. Diese wichtigen Gesetze lauten Kommutativgesetz, Assoziativgesetz und Distributivgesetz. Außerdem muss die Regel Punkt vor Strich beachtet werden. Die Inhalte werden als Text und als Video erklärt.
Starten wir mit einer Definition zu den Rechengesetzen:
Hinweis:
Die drei wichtigsten Rechengesetze der Mathematik lauten Kommutativgesetz, Assoziativgesetz und Distributivgesetz. Mit diesen Rechengesetzen lassen sich viele Aufgaben zur Addition, Subtraktion, Multiplikation oder Division lösen.
Solltest du dich nur für ein bestimmtes Rechengesetz interessieren oder für die Regel Punkt vor Strich, kannst du auch direkt zu diesem Inhalt wechseln:
Rechengesetze für die Addition
Los geht es mit dem Kommutativgesetz: In der Mathematik spielt es keine Rolle in welcher Reihenfolge die Zahlen bei einer Addition stehen. Das Ergebnis der Addition ändert sich dadurch nicht. Ein Beispiel:
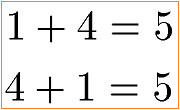
Die Summe ist in beiden Fällen 5. Das man die Reihenfolge von zwei Zahlen verändern kann bezeichnet man in der Mathematik als Kommutativgesetz. Die allgemeine Gleichung um dieses Rechengesetz zu beschreiben wird meistens in dieser Form angegeben.
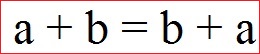
Mehr als zwei Zahlen können ebenfalls in beliebiger Reihenfolge addiert werden. Daher weiter zum Assoziativgesetz: Bei der Addition mit drei Zahlen nennt man dies nicht mehr Kommutativgesetz, sondern Assoziativgesetz. Dabei kann entweder die Reihenfolge der Zahlen vertauscht werden oder durch eine Klammer wird gezeigt, dass erst die Inhalte in der Klammer ausgerechnet werden. Im Beispiel zum Assoziativgesetz der Addition sieht man wie durch die Klammer die Reihenfolge der Berechnung geändert wird. Die Summe ist jedoch immer 9.
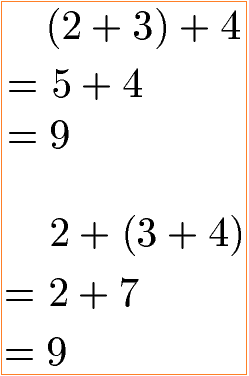
Die allgemeine Darstellung bzw. Formel zum Assoziativgesetz wird oft so aufgeschrieben:
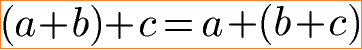
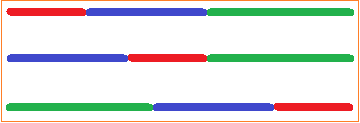
Egal wie viele Zahlen addiert werden sollen: Die Reihenfolge bei nur Additionen spielt keine Rolle. An der Summe ändert sich nie etwas. Kommutativgesetz und Assoziativgesetz können auch grafisch dargestellt werden. Drei Strecken können in beliebiger Reihenfolge aneinander gereiht werden und ergeben dennoch in Summe die gleiche Streckenlänge.
Das Distributivgesetz dient dazu einen Term umzuformen. Eine Möglichkeit besteht darin eine Klammer aufzulösen und eine Summe aus zwei Produkten zu erzeugen. Die Zahl vor der Klammer wird mit jedem Summanden in der Klammer multipliziert. Zum besseren Verständnis ein Beispiel mit Farben:
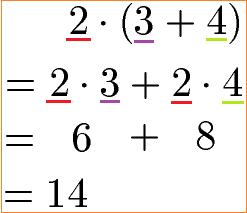
Zur Vollständigkeit noch die zwei allgemeinem Formeln zum Distributivgesetz.
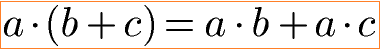
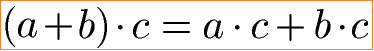
Rechengesetze für die Subtraktion
Bei der Subtraktion dürfen die Zahlen nicht vertauscht werden. Vertauscht man die beiden Zahlen (Minuend und Subtrahend genannt) erhält man eine andere Differenz. Im nächsten Beispiel ändert sich das Ergebnis von +4 auf -4 durch Vertauschen der Zahlen.
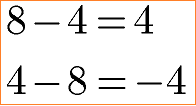
Da die Zahlen in ihrer Reihenfolge nicht vertauscht werden dürfen gilt das Kommutativgesetz für die Subtraktion nicht. Mit der folgenden Ungleichung kann dies ausgedrückt werden.
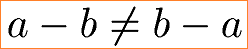
Auch bei mehr als zwei Zahlen darf bei der Subtraktion kein Vertauschen der Zahlen stattfinden. Zumindest nicht wenn man das gleiche Ergebnis möchte. Im nächsten Beispiel wird durch eine Klammer die Reihenfolge der Subtraktion verändert. Mit 6 und 2 führt dies zu unterschiedlichen Differenzen.
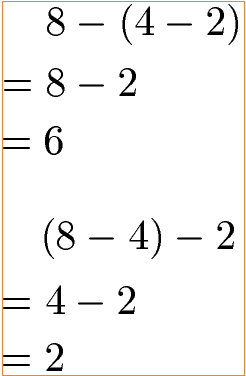
Da die Zahlen nicht vertauscht werden dürfen gilt das Assoziativgesetz für die Subtraktion nicht. Die Ungleichung zum Assoziativgesetz für die Subtraktion lautet damit:
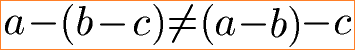
Für das Distributivgesetz gibt es jedoch eine Formel zur Umformung mit einer Subtraktion. Eine Klammer kann eine Differenz aufweisen. Diese Klammer kann durch Ausmultiplizieren mit der Zahl vor (oder nach) der Klammer beseitigt werden. Ein Beispiel:
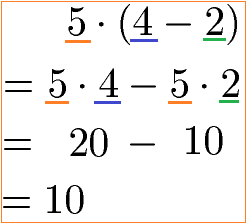
Das Distributivgesetz mit einer Subtraktion kann mit folgender Gleichung beschrieben werden.
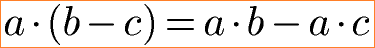
Rechengesetze Multiplikation
Bei der Multiplikation kann ebenfalls die Reihenfolge der Zahlen vertauscht werden ohne das sich das Ergebnis (Produkt) ändert. Die allgemeine Gleichung zum Kommutativgesetz der Multiplikation ist recht einfach.
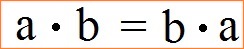
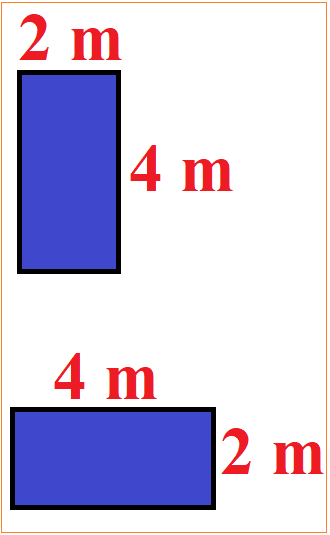
Sehr schön sehen kann man dies bei einer Flächenberechnung. Ein Grundstück ist 8 Quadratmeter groß, selbst dann, wenn Länge und Breite vertauscht werden. Zunächst die Rechnung:
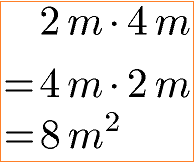
Wird das Grundstück gedreht ändert sich nichts an der Fläche des Grundstücks. Der blaue Flächeninhalt ist in beiden Fällen gleich groß.
Das Kommutativgesetz mit 2 Faktoren kann auf 3 Faktoren erweitert werden. Dies führt uns zum Assoziativgesetz der Multiplikation. Auch hier spielt es keine Rolle, ob einfach von links nach rechts multipliziert wird oder ob eine Klammer gesetzt wird, um eine Multiplikation weiter hinten zuerst zu berechnen. Zunächst die allgemeine Gleichung und danach wieder ein Beispiel.
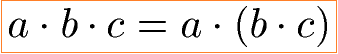
Das nächste Beispiel zum Assoziativgesetz der Multiplikation zeigt das auch eine veränderte Reihenfolge bei den Multiplikationen stets zu 24 als Produkt führt.
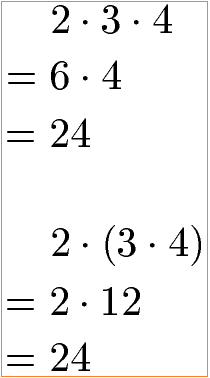
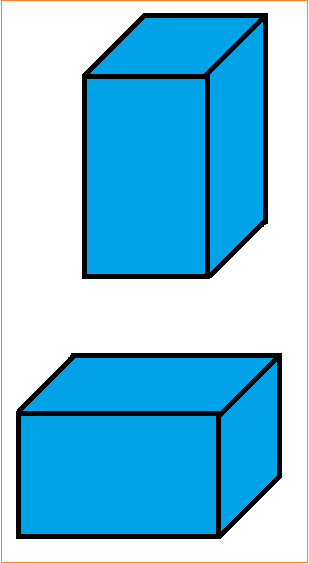
Grafisch kann man sich das mit dem Volumen eines Quaders verdeutlichen. Ändern sich die Seitenlängen eines Quaders nicht, kann dieser beliebig gedreht werden, ohne das sich das Volumen des Körpers ändert.
Das Distributivgesetz kann eingesetzt werden um einen Term ohne Klammer in einen Term mit Klammer zu verwandeln. Kann man bei einer Summe einen gemeinsamen Faktor finden, so lässt sich dieser vor eine Klammer schreiben. Zunächst die - vielleicht etwas verwirrende Gleichung - und danach die hoffentlich besser zu verstehenden Beispiele.
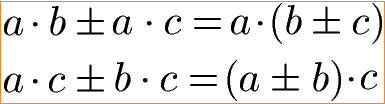
In den beiden Beispielen kommt jeweils die 3 bei jedem Faktor vor. Daher kann diese 3 vor eine Klammer gezogen werden.
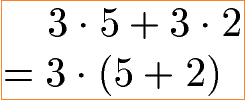
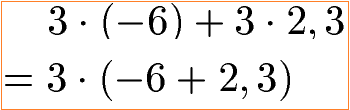
Rechengesetze für die Division
Für die Division gilt das Kommutativgesetz nicht. Werden bei einer Division Dividend und Divisor vertauscht ändert sich das Ergebnis (Quotient) der Aufgabe.
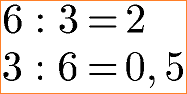
Dies führt uns beim Kommutativgesetz der Division zu einer Ungleichung.
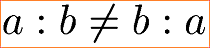
Mehr Zahlen helfen nicht das Problem zu lösen. Auch bei drei Zahlen darf die Reihenfolge der Zahlen bei der Division nicht vertauscht werden. Das Assoziativgesetz gilt daher ebenfalls nicht für die Division und bringt eine weitere Ungleichung.
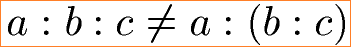
Wer dies nicht Glauben mag findet noch ein Beispiele dafür, dass das Assoziativgesetz für die Division nicht gültig ist.
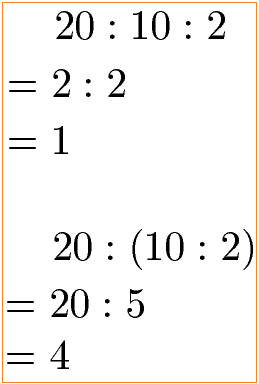
Für das Distributivgesetz zur Division gibt es hingegen eine gültige Gleichung. Diese dient dazu aus einer Summe oder Differenz in einer Klammer geteilt durch c eine Summe oder Differenz ohne Klammer zu erzeugen. Die allgemeinen Gleichungen sind diese:
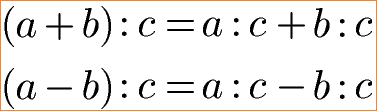
Zum Abschluss noch ein Beispiel zum Distributivgesetz der Division:
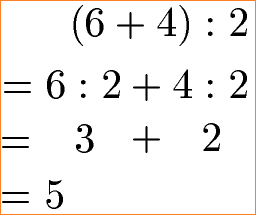
318 Gäste online
Anzeige:
Anzeige:
Verfügbare Fächer:
Anzeige:
Anzeige: